小6算数「場合の数」指導アイデア《組み合わせを落ちや重なりなく調べる方法》

特集: 文部科学省教科調査官監修｢教科指導のヒントとアイデア｣

2022.03.14

単元の展開

第１時　表や図を用いて、リレー選手の並び方がなん通りあるかを、落ちや重なりなく調べる方法を考える。
▼
第２時　条件がある場合（４枚から３枚を選ぶなど）の並べ方がなん通りあるかを考える。
▼
第３時　輪投げして３回投げたときのすべての結果を、◯と×を用いて表す。
▼
第４時（本時）表や図を用いて、アイスクリームの組み合わせを落ちや重なりなく調べる方法を考える。
▼
第５時　表や図を用いて、５種類のお菓子から２種類、または４種類を選ぶ組み合わせを考える。
▼
第６時　組み合わせの考え方を用いて、身の回りの事象（レストランでのメニューの選び方など）について考える。
▼
第７時　練習問題を解いたり、８チームによるトーナメント戦の総試合数について考えたりする。
▼
第８時　練習問題を解き、学習内容に対する理解を深める。

本時のねらい

４種類のアイスクリームから２種類を選ぶ組み合わせについて、順序性がある問題と比較して問題の特徴に気付いたり、図や表を用いたりすることを通して、落ちや重なりなく調べる方法について説明している。

評価規準

順序性がある問題場面との違いに気付いたうえで、４種類のアイスクリームから２種類を選ぶ組み合わせをいくつかの図や表を用いて求めることができる。

食べ放題のアイスクリームコーナーに来ました。４種類の味（バニラ・チョコ・オレンジ・メロン）から２種類を食べます。
（　　　　　　　　　　　　）は、全部でなん通りですか。
※（　）の中には、いろいろな言葉が入ることを伝えましょう。

（　　　　　）の中には、「アイスを食べる順番」という言葉が入ります。答えを求めてみよう。

これまでの問題と同じだ。図や表を使って求めることができます。

答えが分かりました。12通りです。

12通りという答えで合っていますか。

合っています。僕は、図を使って考えました。

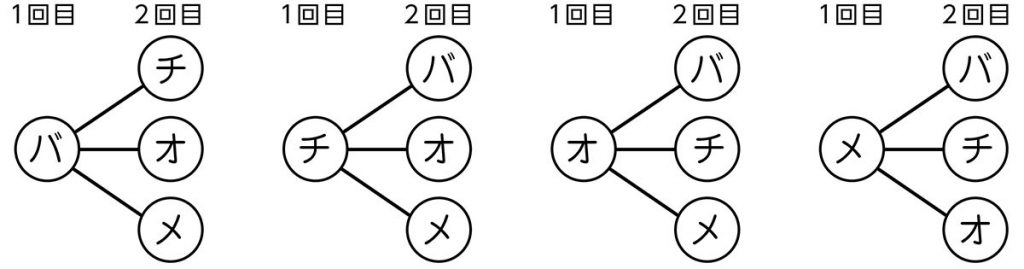
最初にバニラアイスを１回目にしたときが３通りだと分かれば、３×４という計算でも分かるね。

私は、表でも考えてみたよ。

※バ：バニラ、チ：チョコ、オ：オレンジ、メ：メロン

次は、（　　　　）の中に、「アイスの組み合わせ」という言葉が入ります。答えは、なん通りでしょう。

えっ!?　数字は変わってないから、12通りで変わらないと思うけど……。

でも、さっきは「順番」で、今度は「組み合わせ」だよ。だから、答えも違うかもしれない。

「食べる順番」のときとは違って、みんなの意見がまとまりませんね。それでは、今の皆さんの考えについてロイロノートのテキストに書いて提出してください。「12通りでよい」という考えの人は、赤いテキストを提出します。「12通りではない」という考えの人は、青いテキストを提出します。「どちらか決めることができない」という人は、黄色のテキストを提出しましょう。理由がある人はテキストに書いてください。