小6算数「資料の整理」指導アイデア
執筆／東京都公立小学校教諭・肥後和子
編集委員／文部科学省教科調査官・笠井健一、東京都公立小学校校長・長谷豊
目次
本時のねらいと評価規準
本時の位置 5／13
ねらい
度数分布表を柱状グラフ（ヒストグラム）に表して分布の様子をとらえ、データの特徴を読み取ることができる。
評価規準
- 度数分布表をもとに正しくヒストグラムに表している。
- ヒストグラムから資料の特徴を捉えている。
問題
1組、2組、3組の跳んだ回数を表した度数分布表をグラフに表して各クラスの特徴を読み取り、どのクラスがなわとび大会で優勝するか予想しよう。
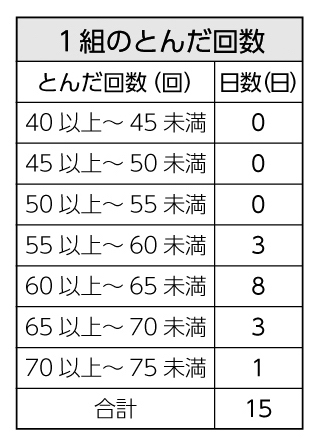
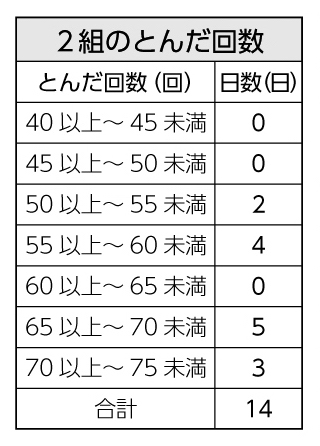
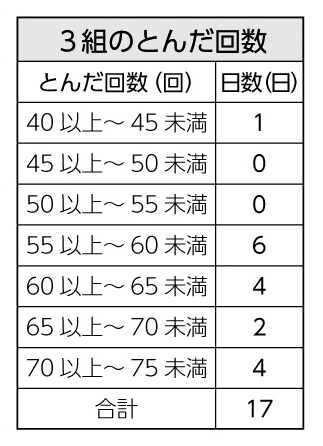
これまでの学習では、平均値、ドットプロット、度数分布表を使ってどのクラスが優勝するかを予想しましたね。今日は、度数分布表をグラフに表し、散らばりの様子から優勝予想をしたいと思います。
どんなグラフになるのかな?
このグラフは度数分布を表す柱状グラフといいます。ヒストグラムともいいます。
―ヒストグラムを知る―
棒グラフと似ているけれど隙間がありません。
その階級に何日あるかをマスの幾つ分で表しています。
2組と3組の度数分布表をヒストグラムに表してみましょう。
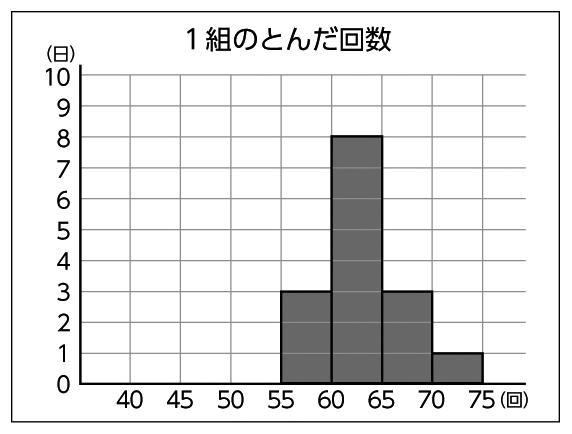
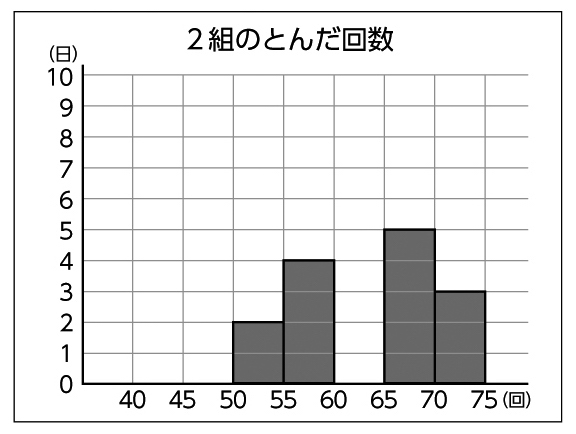
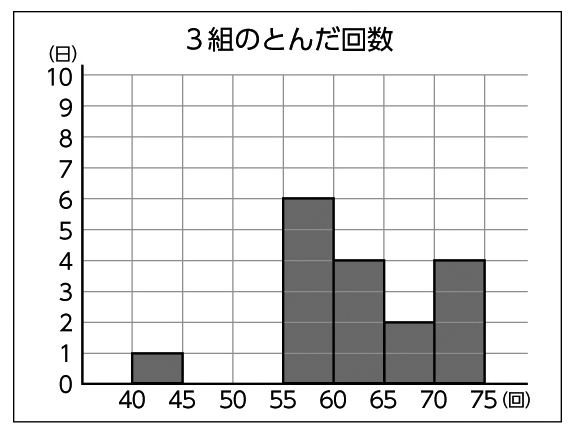
今日はこのヒストグラムをもとに、3クラスの特徴を改めて考え、どのクラスが優勝できそうか考えてみたいと思います。
本時の学習のねらい
柱状グラフ（ヒストグラム）から、3クラスの特徴を読み取ろう。
見通し
ヒストグラムを使うと1組、2組、3組の資料についてどんなことが調べられるかな。
1番多い度数の階級や階級の幅を調べることができます。
全体に占めるある階級の度数の割合を調べることができます。
今までに調べた平均値や最頻値との比較もできそうです。
いろいろな見方で調べることで、より正確な予想ができそうですね。
自力解決の様子
A 自分の考えが説明できない。
反応例：1番多い度数を見ると、1組は60以上65未満、2組は65以上70未満、3組は55以上60未満ということがわかった。
B 資料の大まかな特徴を捉え、自分の考えをまとめている。
反応例：1番多い度数で比べると2組、階級の幅で比べると1組、70回以上の記録で比べると3組の記録がよい。
C 既習事項と関連付けて資料を読み取り、自分の考えをまとめている。
反応例：65回以上75回未満の度数で比べると、1組が4日、2組が8日、3組が6日、これを割合で示すと1組27％、2組57％、3組35％。割合の方が正確かもしれない。
学び合いの計画
イラスト／横井智美
『教育技術 小五小六』2020年12月号より
