小2算数「かけ算(1)」指導アイデア(11/16時)《同数にそろえるよさ》
執筆/富山県公立小学校教諭・細江孝太郎
編集委員/文部科学省教科調査官・笠井健一、前富山県公立小学校校長・中川愼一
目次
本時のねらいと評価規準
(本時11/16時 「2~5の段の九九」の学習の後)
ねらい
数を数える2つの場面を早さと正確さの観点から比べることを通して、同数にそろえるという乗法の特徴とよさについて考える。
評価規準
同数にそろえるよさに着目し、かけ算をものの数を数えるときに生かすことを考えている。(思考・判断・表現)
問題
○の数をできるだけ早く数えましょう。
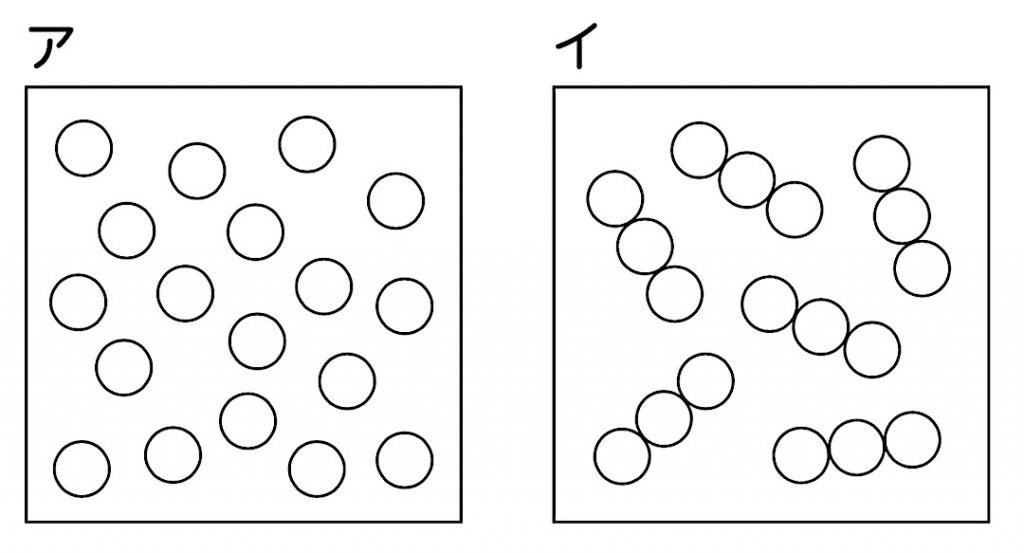
○は何個ありましたか。
アは18個ありました。
イも18個ありました。
アもイも18個でした。
イのほうが数えやすかったです。
僕はアのほうが順に印を付けやすかったです。
イは3の段の九九が使えます。
数が早く正しく分かったのは、アとイのどちらでしたか。
○がばらばらに並んでいるアと、3つずつのまとまりになっているイの2つを提示します。比較することで、それぞれのよさがよりはっきりと子供たちの言葉で語られていきます。
学習のねらい
数が早く正しく分かるのは、アとイのどちらだろう。
見通し
かけ算を使えば早く数えられそうだ。
自力解決の様子
A つまずいている子
アを選択
・○を1つずつ数えている。
B 素朴に解いている子
イを選択
・「3×6=18(さぶろくじゅうはち)」をすれば、1つずつ数えるよりも早いことに気付いている。
C ねらい通りに解いている子
イを選択
・「3つのかたまりが6つだから」など、かけ算を使える理由を述べている。
・かけ算を使うと早く正確であるなど、かけ算を使うよさについて述べている。
学び合いの計画
イラスト/横井智美
『教育技術 小一小二』2020年10月号より






