小6算数「分数のかけ算」指導アイデア《分数に整数をかける計算方法を考えよう》
執筆/埼玉県公立小学校主幹教諭・宮河俊宏
編集委員/文部科学省教科調査官・笠井健一、浦和大学教授・矢部一夫
目次
本時のねらいと評価規準
(本時1/13時)
被乗数が分数の場合の乗法計算の仕方について、乗法の性質や比例の考えを基に考え、数直線や式などを用いて表現している。

問題場面
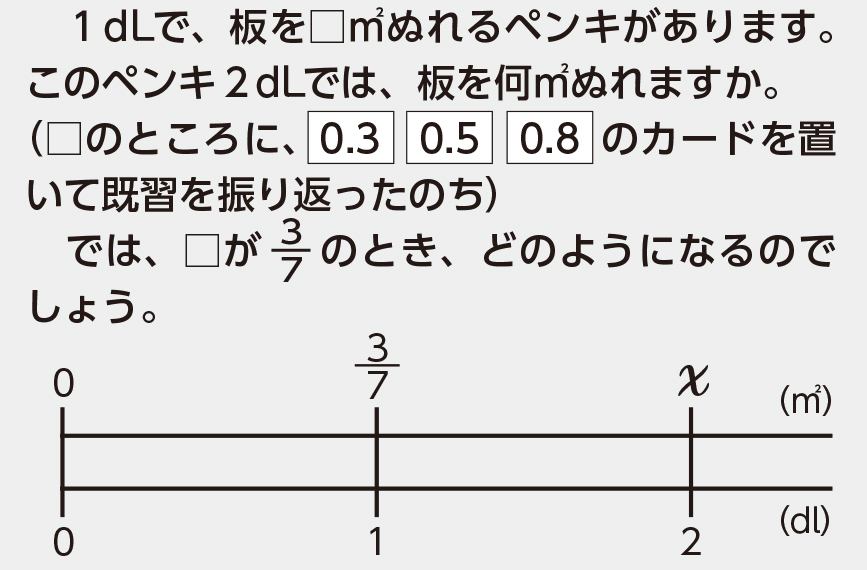
□が小数の場合は、式を立て答えが求められましたね。では、[MATH]\(\frac{3}{7}\)[/MATH]の場合はどうでしょう。
1dL でぬれる面積とペンキの量から、どれだけぬれるかについて考える問題だから、かけ算でいいと思います。式は、[MATH]\(\frac{3}{7}\)[/MATH]×2だと思います。
整数や小数を用いたかけ算は学習したけれど、分数を用いたかけ算は、まだ学習していないよ。かけられる数が分数のときでもかけ算を使えるようになりたい。
では、かけられる数が分数の場合の計算について考えていきましょう。
本時の学習のねらい
分数に整数をかける計算のしかたを考えよう。
見通し
図や数直線に表して求めてみよう。
[MATH]\(\frac{3}{7}\)[/MATH]が2つあるのだから、たし算でもとめられないかな。
[MATH]\(\frac{1}{7}\)[/MATH]をもとにして、「そのいくつ分」で考えてみよう。
自力解決の様子
A 立式はできたが計算の仕方が分からない
かけ算の立式をすることは分かったが、分数を用いたかけ算を行うためには、どのようにすればよいのか分からない。
B かけ算の意味から考えている
かけ算は同じ数を繰り返したすと答えが求められるから。
[MATH]\(\frac{3}{7}\)[/MATH]×2=[MATH]\(\frac{3}{7}\)[/MATH]+[MATH]\(\frac{3}{7}\)[/MATH]=[MATH]\(\frac{6}{7}\)[/MATH]
[MATH]\(\frac{6}{7}\)[/MATH]㎡
C 単位の考えを用いて考えている
[MATH]\(\frac{3}{7}\)[/MATH]は[MATH]\(\frac{1}{7}\)[/MATH]の3つ分だから、[MATH]\(\frac{3}{7}\)[/MATH]×2は[MATH]\(\frac{1}{7}\)[/MATH]の(3×2)こ分になる。
学び合いの計画
立式をして自力解決に入っても、分数を用いたかけ算の計算の仕方について説明することが難しい児童が少なくありません。そこで、既習である整数や小数のかけ算の解法と関連付けたり、面積図や数直線の図と関連付けたりすることで、ペンキの量とぬれる面積の間には比例関係が成り立つことを視覚的に理解できるようにします。
イラスト/横井智美
『教育技術 小五小六』 2021年4/5月号より