小1算数「たし算とひき算」指導アイデア《順序数を集合数に置き換えると、加法や減法が適用できることを理解する》
執筆/福岡教育大学附属福岡小学校教諭・井手恭敬
監修/東京都国立教育政策研究所教育課程調査官・加固希支男、福岡県教育センター指導主事・西島大祐
目次
年間指導計画
・10までの数
・なん番目
・いくつといくつ
・いろいろな形
・あわせていくつ
・ふえるといくつ
・のこりはいくつ
・ちがいはいくつ
・どっちが長い
・整理しよう
・10より大きい数
・何時 何時半
・3つの数の計算
・たし算
・ひき算
・形づくり
・たすのかな、ひくのかな
・20より大きい数
・どっちがひろい
・何時何分
・たし算とひき算
単元の展開(各時の主な学習活動内容)
第1時 (本時)順序数を集合数に置き換えると、加法や減法が適用できることを理解する。
第2時 異種の数量を同種の数量に置き換えると、加法や減法が適用できることを理解する。
第3時 求大の場合について、加法が適用できることを理解する。
第4時 求小の場合について、減法が適用できることを理解する。
第5時 場面を図に表して問題の構造をとらえ、式や言葉を用いて説明することができる。
本時のねらい
順序数を含む場合も、人の数をブロックや図に表すことで、加法や減法が適用できることを理解する。
評価規準
場面に合った数量の関係をブロックや図に表現し、たし算やひき算になることの意味を説明することができている。
本時の教材のポイント
本単元では、順序数や異種の数量を含む場面、求大や求小の場面においても加法や減法が適用される場として判断することができるようにすることが大切です。特に本時では、「順番」と「人の数」に着目しながら、順序数を含む場合も、人の数をブロックや図に表すことで、たし算やひき算の式に表すことができることをねらいとして進めていきます。
導入段階では、「みさきさんは、前から7番目にいます。みさきさんの後ろに3人います。みんなで何人いますか」という問題を提示します。まず「7番目」の中にはみさきさん自身が含まれることを確認しながら、前にいる人数と後ろにいる人数をブロックや図に表し、全体の人数を求める活動を行います。この過程で、順番としての7と、人の数としての7に着目していくことができるようにしていきます。また、「7番目なら前には6人」という数量の関係を説明する場も設定し、数の関係を言葉と図で表すことができるようにします。
展開段階では、問題を「11人並んでいます。あおいさんは前から5番目にいます。あおいさんの後ろには何人いますか」に変えて提示します。ここでは、「何番目」ということが分かっている問題場面であることは似ているけれど、後ろの人数を問われているところが違うということに意識させ、最初の問題と同じようにブロックや図に表現して問題を解決していきます。ブロック操作や図に表現することで、後ろの人数を求める場面にはひき算が適用できることに気付かせていきます。
終末段階では、2つの問題の違いや問題を解決するポイントを子供自身の言葉でふり返らせます。「何番目」という順序数を含む場面もブロックや図に表すことで、集合数に置き換えることができることから、たし算やひき算で表されたことを理解させていきます。
本時の展開
今日の場面です。この絵をよく見ましょう。みさきさんは、前から7番目にいます。みさきさんの後ろに3人います。みんなで何人いますか。(イラストは左から少しずつ見せていく)

どんなことが分かっていますか。
みさきさんが7番目にいます。
みさきさんの後ろには3人います。
そうですね。では、今日は何を調べていきますか。
みんなで何人いるかを調べます。
ブロックや図に表すと、説明できそうです。
どんな式で求めることができるかな。

みんなで何人いるかを求めるには、どんな式になるかブロックや図を使って調べよう。
見通し
前にいる人数と後ろにいる人数に気を付けるとよさそうです。
ブロックや図を使うと、式に表すことができそうです。
自力解決の様子
A つまずいている子
「7番目」をそのまま7人と捉え、前にいる人数とみさきさん本人の区別がついていない。ブロックの数が合わず、全体の人数を正しく表すことができていない。
B 素朴に解いている子
前に6人、後ろに3人いることは理解しているが、みさきさん本人を入れることを忘れ、(6+3)をして9人としてしまっている。
C ねらい通り解いている子
「7番目だから前には6人いる」と説明し、前の6人、みさきさん1人、後ろの3人をブロックや図で表して、(6+1+3)をして10人と正しく人数を求めることができる。
全体発表とそれぞれの考えの関連付け
どのように考えましたか。
7番目ということは、前に6人いて、その後ろがみさきさんです。
その後ろに3人いるので、6人と1人と3人を合わせました。
式に表すと、6+1+3=10です。
みんなで10人いることが分かります。
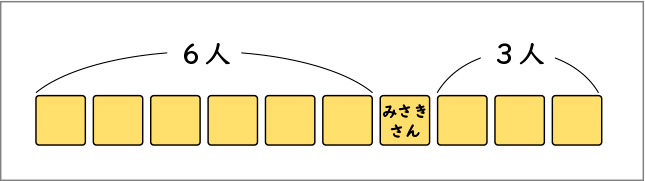
なぜ、前が6人になるのですか。
7番目には、みさきさんが入っているので、前の人は6人になります。
なるほど。順番の数と、人の数が図に表すとよく分かりますね。他にはどのような考え方で調べましたか。
前が7人で、後ろが3人だからこのような図にしました。
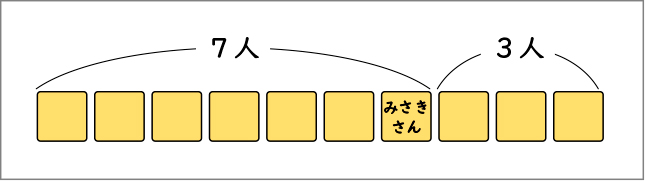
この図を基にするとどのような式になりますか。
7+3=10です。
さっきと同じで、やっぱり全部の人数は10人になります。
図を基にしながら、たし算の式に表すことができましたね。では、次の問題です。

11人 ならんで います。あおいさんは、まえから 5ばん目に います。あおいさんの うしろには、なん人 いますか。
さっきの問題と、似ているところや違うところはありますか。
あおいさんが前から5番目にいることが分かっているところは似ています。
全部の人数はもう分かっています。
今度は、後ろの人数を聞かれています。
この問題もブロックや図に表すと、式にできそうです。
では、この問題もブロックや図を使って考えてみましょう。
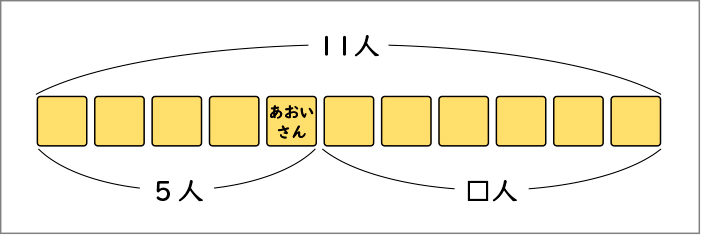
全部で11人だから、11から5を引くと6人になります。
式に表すと11-5=6です。
どうして、ひき算になるのですか。
全体の人数から、前に並んでいる人を引くと、後ろの人数が分かるからです。
前に並んでいる5人の中に、あおいさんも入っています。
評価の視点
構成/桧貝卓哉 イラスト/横井智美・やひろきよみ 図版/永井俊彦

