小4算数「角の大きさ」指導アイデア《三角定規を使って角の大きさを比べてみよう》
執筆/埼玉県公立小学校教諭・秋山泰孝
編集委員/文部科学省教科調査官・笠井健一、浦和大学教授・矢部一夫
目次
本時のねらいと評価規準
(本時の位置 1/10 単元の導入)
ねらい
角の大きさを回転の大きさと捉え、それを任意単位を用いて表そうとする。
評価規準
既習の測定の学習と同様に、角の大きさも単位となる大きさを決めて、そのいくつ分かを数値で表せないかを考えることができる。(数学的な考え方)

問題場面
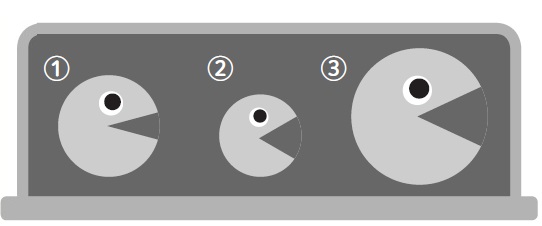
①②③のキャラクターがいます。どのキャラクターの口がよく開いていると言えるでしょう。
口先の幅の長さで比べるのかな。
口の開き具合で比べるほうがよいですね。開き具合は、どうしたら確かめられますか?
重ねて比べます。重ねると、②が一番よく開いています。
三角定規を当ててみます
開けた口の角が大きければ、より開いていると言えるのですね。もう1つ、④のキャラクターがいるのを忘れていました。
キャラクター④
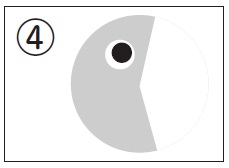
②よりもかなり大きいね。
④の角の大きさは、②の角の大きさより、どれだけ大きいでしょうか?
どれだけ大きいって、どう表せばいいの?
長さや重さのときと同じように、何かのいくつ分と表せないかな。
本時の学習のねらい
角の大きさの違いの表し方を考えよう。
見通し
既習の量の比較経験を問題解決に生かせるよう、長さやかさを比較した際にどのように考えたかをふり返る時間を取ります。
そのなかで、身近なものを基準として、そのいくつ分と考え、数値化し、比較したことを想起させ、角の大きさも同じように考えられないかと発問し、自力解決に入るようにします。
自力解決の様子
※一人ひとりにキャラクターを印刷したシートを配付する。
A つまずいている子
基準とするものが見付けられない。

B 素朴に解いている子
三角定規の複数の角を用いて、比較する。

C ねらい通り解いている子
三角定規の30°を用いて、そのいくつ分で表す。

学び合いの計画
イラスト/小沢ヨマ、横井智美
『教育技術 小三小四』2019年4月号より

