小1算数「ひき算」指導アイデア《13-4の計算の仕方》
執筆/北九州市立熊西小学校教諭・敷田明希
監修/文部科学省教科調査官・笠井健一、福岡教育大学教授・清水紀宏

目次
単元の展開
第1時 「10といくつ」という数の見方に着目し、13-9の計算の仕方を考える。
▼
第2時 「10といくつ」という数の見方に着目し、減数が8や7の場合の計算の仕方を考える。
▼
第3時 減数が9〜5の場合の計算練習や文章題の解決をする。
▼
第4時(本時)「10といくつ」という数の見方に着目し、13-4の計算の仕方を考える。
▼
第5時 11〜18から1位数を引く繰り下がりのある減法の計算練習、文章題の解決をする。
▼
第6〜8時 計算カードを使った11~18から1位数を引く繰り下がりのある減法計算の習熟
▼
第9時 学習内容の習熟・定着
本時のねらい
繰り下がりのあるひき算で、ブロックを用いて計算の仕方を考え、話し合う活動を通して、「10といくつ」に着目し、10から減数を引いたり、減数を分けて被減数から順に引いたりする計算の仕方を考えることができるようにする。
評価規準
13-4などの計算について、10から減数を引いたり、減数を分けて被減数から順に引いたりする計算の仕方を考え、説明することができる。(思考・判断・表現)
本時の展開
※ケーキ作りにたまごを用意している様子を提示する。

今からケーキを作るんだね。
ケーキを作るには、たまごが4個いるんだって。
たまごは13個あるから残りそうだよ。

たまごが 13こ あります。4こ つかうと のこりの たまごは なんこですか。
9個だと思います。
9個という予想が出ていますね。なぜ9個だと思ったのですか。
ひき算をしました。
ひき算だと思ったのはなぜですか。
13個から4個減るので、13-4をするといいと思います。
「のこり」と書かれているからです。
ケーキを作るには、たまごを4個使って、たまごの数は減るからです。
でも右側のパックからは、一度に4個引けません。
本当だ。3個しかないね。
どうやってたまごを4個取るといいのかな。
計算したら分かるかな。

13-4の計算の仕方を考えよう。
見通し
どのようにしたら、計算ができそうですか。
前と同じように、ブロックを動かしたらいいと思います。
13を「10と3」に分けたらいいと思います。
4を「3と1」に分けることもできると思います。
自力解決の様子
A つまずいている子
これまでの学習を生かして、13を分け、「10といくつ」に着目することはできているが、「4から3を引いて1」というように、被減数と減数を入れ替えて、大きい数から小さい数で引くことができるようにひき算をしている。また、指で数えて求めている。
・13を10と3に分ける。4から3を引いて1。10と1で11。
B 素朴に解いている子
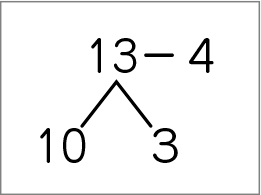
ブロックを10と3に分けて並べて考えているが、端数から減数を1つずつ動かして考えている(数え引き)。
13―4=9 9個
C ねらい通り解いている子
●減加法で考えた子供
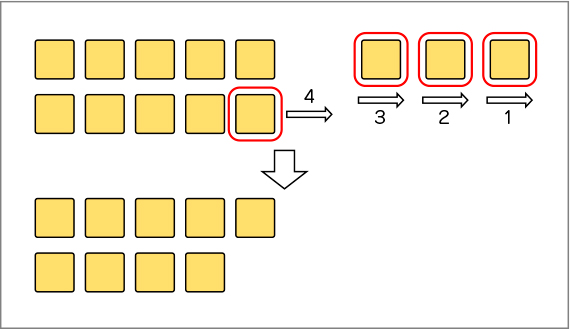
13は10より大きい数なので、「10と3」に分けられることに着目して考えることができている。また、端数の3から減数の4を引くことができないことに着目し、10のまとまりから減数を引くことができている。
・3から4は引けないから、13を10と3に分ける。10から4を引いて6。6と3で9。

●減々法で考えた子供
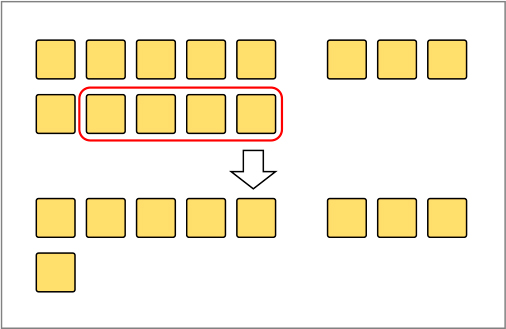
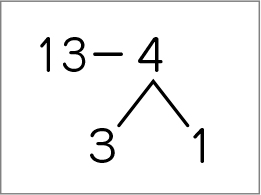
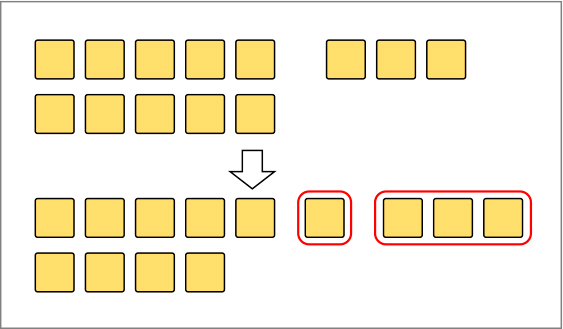
減数を「3と1」に分けて書き、13から3を引くことで「10のまとまり」ができることに着目することができている。その後、10から1を引いて答えを導いている。
・3から4は引けないから、4を3と1に分ける。13から3を引いて10。10から1を引いて9。
学び合いの計画
Aの子供は、ブロックを操作して答えを求めるまでに至っていません。また、「10といくつ」に着目することができていますが、「3-4」ができないので、ひき算ができるように被減数と減数を入れ替えています。「3」は減数の「3個」と認識することができるように、「この考え方は、ブロックを使うと、どのように動かすといいかな」と問いかけ、Bの子供との交流を促します。そうすることで、「3-4」はできないから、10から4を引くとよい、ということに気付くようにします。
Bの子供は、前時までの計算の仕方を13-4に適用することができず、数え引きなどで答えを出しています。「10より大きい数から引くときには、13をどのように分けるとよかったかな」と前の時間の学習をふり返らせるとともに、全体交流の場で、自分の数え引きの方法と減々法を関連付けるようにします。また、Cの式だけ(減加法)で考えた子供との交流を促し、「この式だと、ブロックはどのように動かすとよいのかな」と問いかけます。そうすることで、Cの式だけで考えた子も、ブロック操作を根拠として、説明することができます。
Cの子供は、減加法と減々法で考えています。それぞれの考えで問題解決した子供を意図的に交流させ、ブロック操作や図などを用いて表現し伝え合い、お互いの考えを理解しようとする態度を養います。
ノート例
C ねらい通り解いている子(減加法)

C ねらい通り解いている子(減々法)

B 素朴に解いている子

A つまずいている子

全体発表とそれぞれの考えの関連付け
全体発表では、話合いを通してAとBの考えを、Cの「10のまとまり」に着目した考えへと深めていきます。しかし、初めにAの子供の考え方は提示せず、Bの子供の考えから確認していきます。そうすることで、Aの子供は、自分の考えを修正することができます。子供の実態をふまえて、Bの子供の考え方を全体で確認した後、ペア学習や小集団学習を通して、Aの子供にBの考え方を説明させてもよいでしょう。
Bの子供の考えを確認した後、Cの子供(減加法)を指名し、「10のまとまり」に着目した考えを確認します。その後、Cの子供のブロック操作を式で表します。さらに、減々法で考えた子供の考えを確認します。 どの考え方も導入で予想していた「9」という答えになるので、その答えが正しいことを確認します。その後、教師からAの子供の考えを提示します。「答えが9ではないから11が誤り」という話合いではなく、Aの子供の考えのどこに問題があるのかを考えていくようにします。このAの子供の考え方について考えることで、被減数を「10といくつ」に分けたり、減数を分けて10から順に引いたりする考え方の理解にもつながります。
●数え引き
まず、Bさんの考えを発表してもらいましょう。
イラスト/横井智美

