小３算数「式と計算」指導アイデア《加法と乗法が混じった問題の２通りの解決方法を考える》
執筆／東京都目黒区立碑小学校教諭・大村英視
監修／文部科学省教科調査官・笠井健一、東京都目黒区立八雲小学校校長・長谷豊
目次
単元の展開
第１時（本時）加法と乗法を組み合わせた問題
▼
第２時 減法と乗法を組み合わせた問題
本時のねらい
加法と乗法の混じった問題について、多様な方法で問題解決ができる。
評価規準
加法と乗法の混じった問題を、鉛筆と鉛筆キャップの代金を別々に求めて後から足す方法と、鉛筆と鉛筆キャップ１組分の代金をまとめてから全体の代金を求める方法を考え、説明している。
本時の展開
６人でお楽しみ会をします。お楽しみ会ではジュースとスナックを配ります。そのために、70円のジュースを６本と、30円のスナックを６ふくろ買いました。代金は合わせて何円ですか。
※上の問題を提示し、全体で場面を確認する。イラストを提示するなど、問題場面を具体的にイメージできるようにします。
どのようにすれば代金が分かりそうですか。
ジュース６本の代金とスナック６袋の代金を求めて、足せばよいと思います。
ジュースとスナックをセットで考えても代金を求められると思います。
ジュースとスナック全体の代金を求める方法を考えよう。
自力解決の様子
A つまずいている子
問題場面は把握できても、解決の方法が見付からない。
Ｂ 素朴に解いている子
１つの方法で解決し考えを説明している。
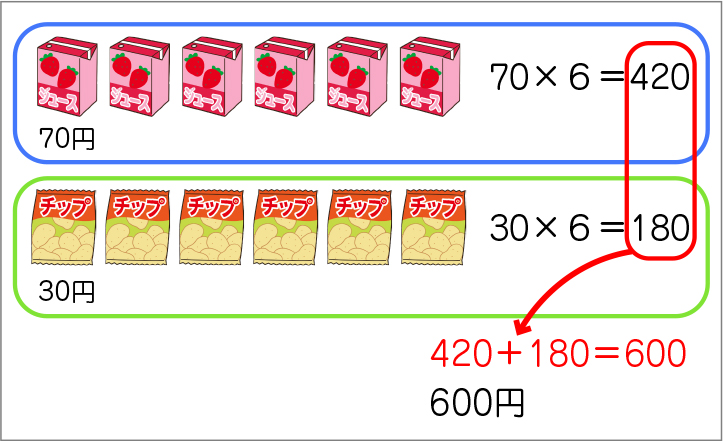
・それぞれの６人分の代金を求め合わせている。
70×６＝420
30×６＝180
420＋180＝600
・１人分を求め、それを６倍している。
70＋30＝100
100×６＝600
Ｃ ねらい通り解いている子
２つの方法で解決し、考えを説明している。
・それぞれの６人分の代金を求め合わせている。
70×６＝420
30×６＝180
420＋180＝600
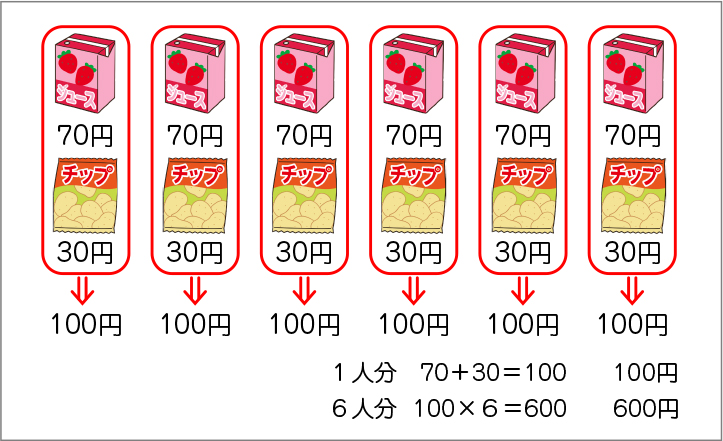
・１人分を求め、それを６倍している。
70＋30＝100
100×６＝600
学び合いの計画
自力解決ではジュース６本分とスナック６袋分の代金を別々に計算してから合計の代金を求める方法で解決する子供のほうが多いことが予想されます。
検討場面では解決のための式のみを提示し、式の意味を考える時間を設けます。その際、授業支援アプリを活用して、ジュースやスナック菓子のイラストや模擬貨幣の素材を全体で共有しておけば、子供はそれらを複製することで、提示された式の意味を簡単に表現することができます。
式の意味を確認する際には、どちらの考えについても、自力解決の段階ではその方法で解決していなかった子供に、授業支援アプリに投稿された画面を用いて説明させるとよいです。
それぞれの解決方法について、多くの子供が理解できているようであれば、全体で共有した子供の図を一人一人の学習用情報端末に配付し、その図を用いてペアで解決方法を説明する時間を設けます。
考え方を理解している子供が少ないようであれば、全体の場で数人の子供にヒントになることを発言させ、それを全体で解釈していくことで子供も式の意味を自分で説明できるようにします。
ノート例
A つまずいている子
自力で解決できない子供には、ジュース６本とスナック６袋のイラストを提示し、それぞれの代金を確認することで、合計の代金を求められるようにします。
イラスト／横井智美、やひろきよみ
-
小４理科「人の体のつくりと運動」指導アイデア
-
小５国語科「浦島太郎 『御伽草子』より」全時間の板書＆指導アイデア
-
小２国語科「なかまのことばとかん字」全時間の板書＆指導アイデア
-
小４理科「雨水の行方と地面の様子」指導アイデア
-
小４理科「季節と生物（夏の終わりと秋）」指導アイデア
-
小１国語科「しらせたいな、見せたいな」板書例＆全時間の指導アイデア
-
小６算数「円の面積」指導アイデア《円の求積公式を用いて、複合図形の面積を求める》
-
小６算数「分数×分数」指導アイデア《乗数の分子が１のときの分数×分数の計算の仕方を考える》
-
小３算数「棒グラフと表」指導アイデア《目的に応じた資料を集め、分類整理し、表に表す》
-
小５算数「単位量あたりの大きさ」指導アイデア《単位量あたりの考え方について知る》
