小3算数「計算の順序」指導アイデア《乗法の結合法則の理解と計算への活用》

執筆/お茶の水女子大学附属小学校教諭・岡田紘子
監修/文部科学省教科調査官・笠井健一、東京都目黒区立八雲小学校校長・長谷豊

目次
単元の展開
第1時(本時)数量の関係に着目し、乗法の結合法則が成り立つことを理解し、これを用いて計算することができるようにする。
本時のねらい
計算の順序について、乗法では結合法則が成り立つことを理解し、3要素2段階の問題を1つの式に表して計算することができ、生活や学習に活用しようとする。
評価規準
・乗法では結合法則が成り立つことを理解し、活用することができる。
・( )を使って式に表すよさに気付いている。
本時の展開
クッキーの箱が5箱あります。全部でクッキーは、何枚ありますか。

1つの箱の中には、クッキーが何枚入っているのですか。
箱の中を見せますね。

袋の中には、3枚ずつクッキーが入っています。全部でクッキーは何枚でしょうか。式を書いて考えてみましょう。
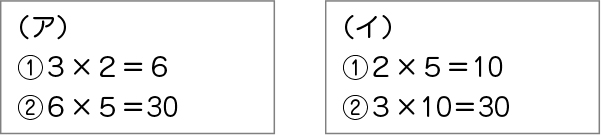
【(ア)の考え】僕は3×2=6 6×5=30と考えて、30枚だと思います。
【(イ)の考え】私は2×5=10 3×10と考えました。答えは30枚です。
2人とも式は違うけれど、同じ30枚になりましたね。2人は、どんな順番で考えたのでしょうか。まず、(ア)の式から考えてみましょう。
3×2の式は、3枚入りのクッキーが2袋あるということだから、1箱分のクッキーの数を表しています。
最初に、1箱分のクッキーの数を求めたのですね。
6×5の式は、1箱に6枚入っていて、その箱が5箱あるということを表しています。
この2つの式を1つの式にまとめることができます。
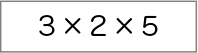
(イ)の式はどんな順番で考えているのでしょうか。
袋の数を先に求めています。
(イ)の式も、(ア)の式のように1つの式に書くことはできないかな。

(イ)の考えを1つのかけ算の式に書こう。
見通し
3枚入りのクッキーが10袋あるということだから、(イ)の②の式は3×10と考えているのかな。
1袋分のクッキーの枚数×袋の数で考えると、袋の数は2×5で求めたから……。
自力解決の様子
A つまずいている子
立式ができない。または、2×5=10×3=30と2つの式を誤って等号で結んでいたり、2×5×3と掛ける数の順番が場面と合っていなかったりする。
B 素朴に解いている子
3×2×5と、( )をつけない式をかいている。
C ねらい通り解いている子
3枚のクッキーが(2×5)袋あることを理解し、3×(2×5)とかけている。
学び合いの計画
自力解決では、2×5=10×3=30と2つの式を誤って等号で結んで書いていたり、2×5×3と掛ける数の順番が場面と誤った式表現をしていたりすることに気が付いていない子もいることと思います。そのような場合は、ノートに絵や図をかくように声かけをし、何がいくつ分あるのか気付かせていくとよいでしょう。
発表・検討場面では、3枚入りの袋が10袋あるという場面と照らし合わせながら、3つの数のかけ算の式を確認していくようにします。また、考え方が違う2つの方法を見比べて、同じ場面のクッキーを求めており、答えは同じ30枚になることから、3×2×5=3×(2×5)と等号で結び、等しいことをまとめていきます。
式のなかの( )は、ひとまとまりの数を表していて、先に計算することができたことは、2年生で( )を使ったたし算でも学習しています。
本時では、「かけ算でも多くの数を掛けるときには計算する順序を変えても答えは同じになること」を、場面と結び付けながらていねいに式に表していくことで理解できるようにしていきましょう。
そして、多様な式の表し方に関心をもたせ、いろいろな方法で場面を式に表現し、式に表すよさに気付いていけるようにしていきましょう。
ノート例
B 素朴に解いている子

A つまずいている子

全体発表とそれぞれの考えの関連付け
(イ)の①の式2×5=10は、何を表している式ですか。
イラスト/横井智美、やひろきよみ

