分数の５つの用い方を理解しておく 【｢系統」を見通し、学年ごとに押さえる！ つまずきなしの「分数」指導法 #1】

分数は昔から理解のむずかしい内容だと言われてきましたが、近年の全国学力調査の結果を見ても、その状況が大きく改善されているとは言えないかもしれません。そこで、２年生から始まる分数の指導をどのように改善していけば、すべての子供たちが分数を理解し、多様な問題解決に活用することができるようになるのか、算数指導について多数の著作をもつ、新潟県新潟市立上所小学校の志田倫明教諭に具体的な説明をお願いしました。
第１回は、なぜ子供たちにとって分数の理解はむずかしいのか、２年～６年の学習を概観しながら分かりやすく説明していただきます。

理解のむずかしさの原因は、分数の使われ方の多様性による

分数を指導しながら子供たちの様子を見ていると、理解のむずかしさの主な原因は、分数の使われ方の多様性にあると思います。分数は用い方が多様で、子供たちはそこで混乱するのです。例えば、分数を割合という見方で理解している子供が、量という意味で使われると混乱して分からなくなったり、逆に量として見ている子供が割合の意味で使われると、それが理解できなくなる原因となったりします。子供は自分が知っている意味で使おうとするのですが、それとは違う使われ方に出合うと非常に混乱するのが分数の一番のむずかしさです。

実際に全国学力調査の問題で分数の正答率が低いと言われますが、誤答例を見てみると、例えば量の問題なのに割合として捉えてしまっているようなものが見られます（資料１参照）。つまり、分かっていないわけではないのですが、一面的な分かり方をしており、問題の場面に合わせて使い分けることができないのです。

【資料１】　平成22年度全国学力調査の結果を踏まえた授業アイディア例より

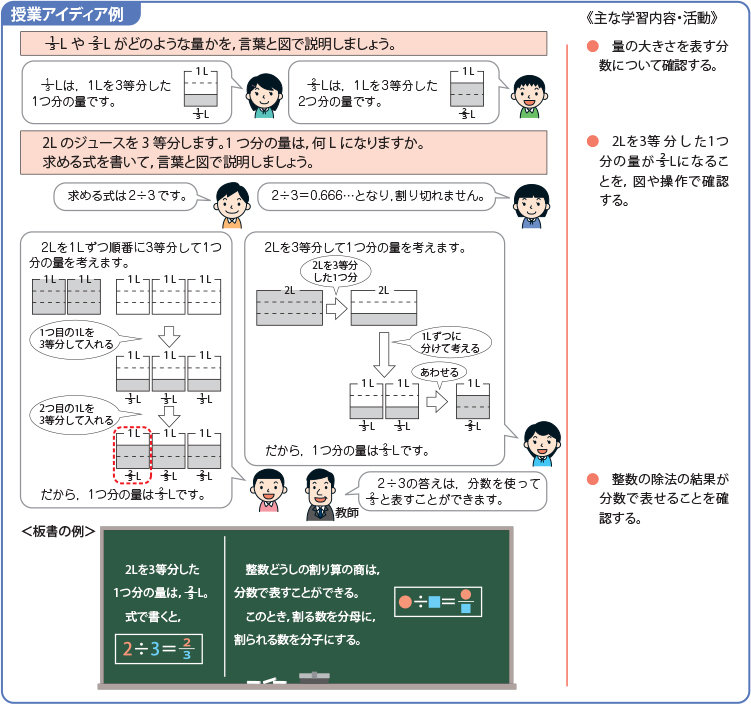
学習指導要領解説では、分数の用い方によって分割分数、量分数、単位分数、割合分数、商分数などと分類されています（学習指導要領解説p153及び245の例①～⑤）。一方、解説の第２章第２節には　算数科の内容の１の⑴に、算数科の内容の骨子が示されていますが、｢数と計算」の領域について詳しく説明された①を見ると、｢算数科では、自然数の概念と分数や小数で表現される数（有理数）の概念について理解するとともに、その表現方法を学習する」とあります（p34）。つまり、分数は小数と同様に有理数の表現形式の一つであるということです。

では、有理数としての分数の表現形式の意味は何かというと、大きく２つあります。第一義は「１を○等分したいくつ分」つまり、[MATH]\(\frac{3}{4}\)[/MATH]は１を４等分した３つ分というようなことで、第二義は「整数を整数で割った商」で、[MATH]\(\frac{3}{4}\)[/MATH]は３÷４の商です。この２つの意味を学ぶことが大前提としてあり、これに類する内容が、６年生の内容における分数の乗法、除法に関する解説の中に示されています（資料２参照）。

【資料２】学習指導要領解説【算数編】p288より抜粋

分数の意味や表現に着目することとは、分数の意味に基づいて [MATH]\(\frac{a}{b}\)[/MATH]を [MATH]\(\frac{1}{b}\)[/MATH]×ａと捉えたり、ａ÷ｂ を [MATH]\(\frac{a}{b}\)[/MATH]とみたり [MATH]\(\frac{a}{b}\)[/MATH] を ａ÷ｂ とみたりするなど分数を除法の結果と捉えたりすることなどである。

この解説の記述の前半が第一義、後半が第二義の説明となる。

分割分数、量分数、単位分数、割合分数、商分数の５分類