小５算数「整数の性質」指導アイデア《公倍数の求め方》

特集: 1人1台端末時代の｢教科指導のヒントとアイデア｣

2023.12.04

単元の展開

第１時　２つに分けられた整数の特徴に着目し、その分け方を考える。
▼
第２時　整数が２で割り切れるかどうかに着目し、整数が偶数と奇数に類別できることを知る。
▼
第３時　偶数と奇数を乗法の式に表し、その意味や性質を考える。
▼
第４時　倍数の意味を理解する。
▼
第５時　公倍数、最小公倍数の意味を理解する。
▼
第６時（本時）公倍数の意味や性質に着目し、公倍数の求め方を考える。
▼
第７時　２つの数の公倍数の求め方を基にして、３つの数の公倍数の求め方を考える。
▼
第８時　約数の意味を理解する。
▼
第９時　公約数、最大公約数の意味を理解する。
▼
第10時　公倍数の意味や性質に着目し、公約数の求め方を考える。
▼
第11時　公約数を活用し、問題を解決する。
▼
第12時　学習内容のふり返りと定着。

本時のねらい

公倍数の意味や性質を基にして、２つの数の公倍数の求め方を考える。

評価規準

２つの数の公倍数は最小公倍数の倍数になっていることに着目し、公倍数の求め方を考えている。（思考・判断・表現）

本時の展開

６と８の公倍数を見付けましょう。

今日は、６と８の公倍数を見付けましょう。

公倍数とは、２つの数の共通の倍数だったね。

前の時間に学習したけれど、６と８の公倍数とは、６の倍数にも８の倍数にもなっている数だね。

でも、６と８の公倍数はどうやって見付ければいいのかな。

６の倍数と８の倍数を全部書き出せばいいよ。

いや、書き出すのは時間がかかるから、工夫すればいいんじゃないかな。

どのように公倍数を見付ければいいのかな。

公倍数の見付け方を考えよう。

見通し

６と８、それぞれの倍数を考えてから共通の数を見付ければよさそうだ。（方法の見通し）

６と８の倍数を全部書き出さなくても、簡単に求める方法がありそう。（方法の見通し）

自力解決の様子

A　つまずいている子

公倍数の見付け方が分からず、それぞれの倍数を書き出している。

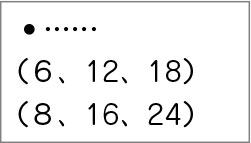
Ｂ　素朴に解いている子

６と８の積で最小公倍数を求めることができると考えている。

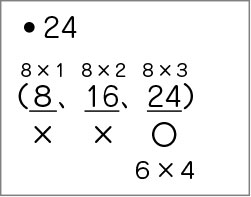
Ｃ　ねらい通り解いている子

最初に、数の大きい８の倍数を書き出す。そのなかから、６の倍数かどうか検討している（〇×を書く）。

学び合いの計画

本単元では、整数の性質について理解し、整数を偶数や奇数に類別したり、倍数や約数などの数の構成について考えたりする力を育んでいきます。

本時の学習では、公倍数の意味や性質に着目し、公倍数の求め方を考えることが大切です。全員が同じ土台で学びを進めていくことができるように、前時までに学習した倍数や公倍数の意味を確認しながら授業を展開していきましょう。

その際、公倍数を求める方法を見いだそうとする子供だけでなく、「もっと簡単な公倍数の求め方もあるのではないかな」とより簡単な求め方を見いだそうとする子供の姿を捉えておくことで、子供のつぶやきを拾って問い返したり、後半の話合いで考えを引き出したりすることができます。

子供一人一人の考えに寄り添いながら、主体的に学びに向かう姿を大切にして授業を展開していきましょう。

ノート例

Ａ　つまずいている子

Ｂ　素朴に解いている子

全体発表とそれぞれの考えの関連付け

どのように公倍数を求めればよいのですか。

前の学習では、｢３と４の公倍数」を見付けたとき、12の倍数だと分かりました。なので、今回も同じように考えて、｢６と８の公倍数」は６×８＝48なので、48の倍数を考えればよいと思います。

ちょっと待って！　公倍数の見付け方は、２つの数をかけ算して求めてはいけないと思うよ。

僕は、６と８の倍数をそれぞれ順番に書き出しました。

そのなかから同じ数を見付けて求めると、６と８の公倍数は24、48、72……と、最小公倍数24の倍数になることが分かりました。

本当だ！　ただ２つの数をかけ算して求めてはいけないんだね。

私も答えは同じです。でも、求めるときに時間がかかってしまう……。

求めやすい考え方は何か考えているんですね。

〈○○さん〉私は、求め方が少し違います。まず８の倍数を調べて、そのなかから６の倍数になっている数を見付けました。

〇〇さんの考え方のほうが簡単に求められるね。

６の倍数から調べてもいいのではないですか。

〈○○さん〉６の倍数から調べてもできます。でも、書き出すとこのようになって、公倍数を見付けるのに少し時間がかかってしまいます。

大きい数の倍数から書き出したほうが、公倍数を見付ける時間が早くなるということだね。

この考え方のほうが、最小公倍数24をすぐに見付けることができるね。

よりよい考えを見付けることができましたね。では、６と８の公倍数を見付けるには、どのように公倍数を求めればいいのですか。

６と８の最小公倍数24を見付けて、その倍数を求めればいいです。そのとき、最小公倍数は、大きい数の公倍数から書き出したほうが簡単に求められます。

前時（３と４の公倍数は12の倍数である）の学習経験から、２つの数の積が公倍数となると誤認識している子供たちがいます。

そのため、考え方を認めつつ、どうして２つの数の積で求めてはならないのか、実際に６の倍数と８の倍数を書き出す友達の考えを扱いながら、理解を深めていく過程を大切にしていきましょう。

話合いでは、考えを共有し合い、自分の考えと友達の考えを比較し合う場を設けましょう。

｢○○さんと同じ考え方だ」｢僕も○○に注目したよ」｢自分とは違った考え方だ」など、友達の考えから、自分では見いだせなかった公倍数の求め方に気付く姿が生まれます。

また、子供がより簡単な方法に着目するつぶやきがあった際、そのつぶやきをしっかり拾い、｢求めやすい方法を考えているのですね」｢もっと求めやすい方法があるの？」など、簡潔性につながる発問を全体に投げかけましょう。

すると、｢あるよ！　だって……！」｢もっと……のほうがいいと思うよ！　だって……！」と、意欲的に発言しようとする子たちが出てくるでしょう。そして、それぞれの考えを聞き、追体験していくことで、より求めやすい方法を見いだしていくことができます。

また、｢６の倍数を書き出した後、８の倍数かどうか考える」方法がより簡単に求められると気付くことができるように、あえて「８の倍数を書き出した後、６の倍数かどうか考える」方法ではダメなのか全体に問い返したことで、図を使って考えを表現する場を設けることができるので、それぞれの考えの違いが明確になり、考えのよさを理解することができます。

その際、ICT機器を使って考えを比較し合うことで、互いの考えのよさをしっかり理解することができます。また、自分の考えを１人１台端末に入力する場を設けることで、教師は子供一人一人の考えを把握し、円滑に話合いを進めていくこともできます。

学習のまとめ

６と８の公倍数は、24、48、72……　←最小公倍数（24）の倍数
24の見付け方は、６の倍数のなかから８の倍数を探すよりも、８の倍数のなかから６の倍数を見付けるほうが見付けやすい。

公倍数を見付けるには、大きいほうの数の倍数から最小公倍数を見付けるとよい。
最小公倍数の倍数が、２つの数の公倍数となる。

評価問題

子供に期待する解答の具体例

①45、90、135
・チャレンジ問題の解答
②21、42、63
③10、20、30

本時の評価規準を達成した子供の具体の姿

２つの数の公倍数は最小公倍数の倍数になっていることに着目し、公倍数の求め方を考えている。

感想例

２つの数の公倍数を見付けるには、２つの数の最小公倍数を求めて、その倍数を考えればよいことが分かりました。
６の倍数と８の倍数を調べていくなかで、24は６の倍数でもあり、８の倍数でもあることが分かりました。
24の倍数である48、72……も６の倍数でもあり、８の倍数でもあると考えました。
倍数や公倍数の学習から、音楽のリズムのような感じをもちました。正しさと美しさはつながりがあるんだなと思いました。
２つの数の公倍数を見付けることができたので、今度は３つの数の公倍数も見付けてみたいです。
九九表のなかには倍数や公倍数がつまっているはずです。倍数や公倍数の見方で九九表を見直してみたいと思いました。

＜導入の工夫＞
時間にゆとりがある場合や子供たちの実態に応じて、次のようなゲームを取り入れる方法もあります。
【パチパチゲーム】
⑴学級を２つのグループに分ける。
⑵それぞれのグループの数を決める。
⑶みんなで数を１から順に唱えていき、自分のグループの数の倍数で手を叩く。
＜ゲーム１＞
Ａグループの数を「３｣、Ｂグループの数を「４」と決めて、ゲームを行う。
＊このとき、グループの代表者に音楽の指揮者のように、それぞれ三拍子、四拍子のタクトを振らせると盛り上がります。また、倍数を見付けにくい子への支援にもなります。
＜ゲーム２＞
Ａグループの数を「６」、Ｂグループの数を「８」と決めて、ゲームを行う。

ワークシート（ダウンロード可）

ダウンロードはこちら＞＞