小6算数「分数×分数」 指導アイデア《小数と分数が混じったかけ算の仕方》
執筆/福岡教育大学附属小倉小学校教諭・本田龍一朗
監修/文部科学省教科調査官・笠井健一、福岡教育大学教授・清水紀宏

目次
単元の展開
第1時 乗数の分子が1のときの(分数)×(分数)の計算の仕方を考える。
▼
第2時 乗数の分子が1以外のときの(分数)×(分数)の計算の仕方を考える。
▼
第3時 乗数が仮分数の計算の仕方を考える。
▼
第4時 帯分数や整数が入った分数のかけ算の計算の仕方を考える。
▼
第5時(本時)(小数)×(分数)、(分数)×(小数)の計算の仕方を考える。
▼
第6時 1より小さい分数を掛けると、積は被乗数より小さくなることを理解する。
▼
第7時 (分数)×(分数)×(分数)の計算の仕方を考える。
▼
第8時 長さが分数で表されている長方形の面積と直方体の体積を求める。
▼
第9時 交換法則や結合法則、分配法則が、分数の計算にも適用できるか考える。
▼
第10時 積が1になる乗数を見付け、被乗数の乗数との間のきまりを見付ける。
▼
第11時 練習問題を解き、学習内容の理解を深める。
本時のねらい
小数×分数で求められる場面について、小数の計算や分数の計算に帰着する方法を比較することを通して、分数の乗法に帰着して求める方法でいつでも計算できることを理解させる。
評価規準
小数、分数が混じった乗法を分数の乗法に帰着して計算することができる。(知識・技能)
本時の展開
※問題場面①を提示する。

へいにペンキをぬります。このペンキは、1dLあたり[MATH]\(\frac{2}{5}\)[/MATH]㎡ぬれます。このペンキ[MATH]\(\frac{1}{3}\)[/MATH]dLでは、何㎡ぬれますか。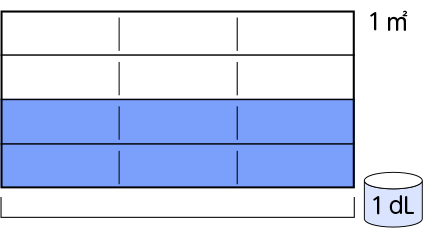
式は言えますか。
[MATH]\(\frac{2}{5}\)[/MATH]×[MATH]\(\frac{1}{3}\)[/MATH]です。
数直線も確認しておきましょう(下の数直線を提示する)。計算するといくつになりますか。
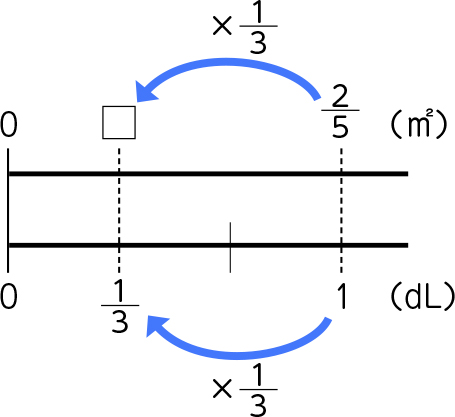
[MATH]\(\frac{2}{15}\)[/MATH]です。
[MATH]\(\frac{2}{15}\)[/MATH]をどのような計算で求めましたか。
分母どうしと分子どうしを掛けました。
掛ける数に3を掛けて1にした後、3で割る方法もありました。
では、この問題はどうでしょう。

へいにペンキをぬります。このペンキは、1dLあたり0.8㎡ぬれます。このペンキ[MATH]\(\frac{1}{4}\)[/MATH]dLでは、何㎡ぬれますか。
問題①と問題②はどこが違いますか。
塗る面積が[MATH]\(\frac{2}{5}\)[/MATH]㎡から0.8㎡に変わりました。
ペンキの量も[MATH]\(\frac{1}{3}\)[/MATH]dLから[MATH]\(\frac{1}{4}\)[/MATH]dLに変わっています。
小数と分数が混じっていても計算できるのかな。
掛けられる数が変わっても、式は×分数になると思う。
すごいことに気付きましたね。ではどんな式になりますか。
0.8×[MATH]\(\frac{1}{4}\)[/MATH]です。
この場面の数直線も確認しましょう。式は0.8×[MATH]\(\frac{1}{4}\)[/MATH]でよいですね。それでは、どうやって計算すればいいでしょうか。
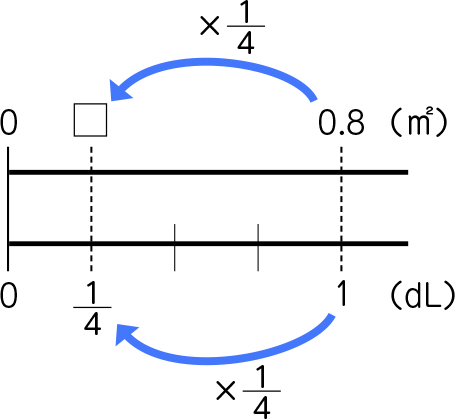
前の学習で考えた等分する方法が使えると思います。
小数を分数にすればよいと思います。
分数を小数にしてもできると思います。
見通し
図で分ける、等分する、小数を分数にする、分数を小数にする

小数と分数が混じったかけ算の求め方を考えよう。
導入では、既習の分数×分数の問題(問題場面①)を取り上げ、大型テレビに面積図を提示しながら、前時までに学習した「等分して求める方法」や「分母どうし分子どうしを掛けて求める方法」をふり返っておきます。
その後、本時の問題(学習場面②)を提示し、既習との違いに気付くことができるようにします。
問題場面が分数×分数から小数×分数に変わったことに目を付けた子供がいれば称賛し、立式します。
既習と未習のずれを意識する提示の仕方を工夫することで、「小数と分数が混じったかけ算はどのように求めればよいのだろうか」という問いを共有することができます。その後、どうすれば解決できそうか、既習の使えそうな考え方を出し合います。
このように、見通しの段階では、前時との違いに目を付けたり、自分の考えをもてそうだという意欲を引き出したりすることで、本時で解決したいことを明確にすることができるようにします。
1人1台端末活用アイデア
下のような図を配付し、導入で見通した等分のイメージをもてるようにします。
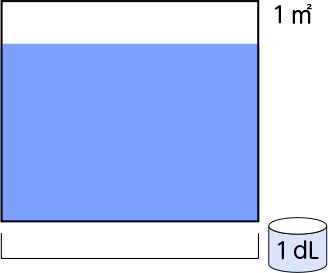
単純に縦に4分割している子供や0.1㎡ずつに分けた後に4等分して40分の1のいくつ分かで考えている子供など、答えは同じでも、それぞれに考えの根拠としている図や式の表現が異なります。
等分した結果やノートに記述した解決方法を写真に撮ってGoogle Classroomやロイロノートなどで共有することで、自分とは違う友達の解決方法を尋ねに行ったり、加筆修正したりするなど、個人思考だけに留まらず、目的をもって他者との交流を促すことができます。
また、つまずいている子には、一度ほかの友達の解決方法を見るよう促し、解決のきっかけをつかむようにしてもよいでしょう。
自力解決の様子
A つまずいている子
0.8を分数で表す方法や[MATH]\(\frac{1}{4}\)[/MATH]を小数で表す方法が分からず、計算を進めることができない。
B 素朴に解いている子
小数の計算で解決する。
・0.8を4等分すればよい。
0.8÷4=0.2 0.2㎡
・分数を小数に直せばよい。
0.8×[MATH]\(\frac{1}{4}\)[/MATH]=0.8×0.25=0.2 0.2㎡
C ねらい通り解いている子
分数×分数で解決する。
0.8×[MATH]\(\frac{1}{4}\)[/MATH]=[MATH]\(\frac{8}{10}\)[/MATH]×[MATH]\(\frac{1}{4}\)[/MATH]=[MATH]\(\frac{8}{40}\)[/MATH]=[MATH]\(\frac{1}{5}\)[/MATH] [MATH]\(\frac{1}{5}\)[/MATH]㎡
学び合いの計画
0.8×[MATH]\(\frac{1}{4}\)[/MATH]という本時の問題に対して、見通しで(分数)×(分数)や(小数)×(小数)に帰着する(持ち込む、直す)ことを確認していますが、Aの子供のように、0.8を分数で表したり、[MATH]\(\frac{1}{4}\)[/MATH]を小数で表したりすることができない子供もいるかもしれません。
0.8が0.1の8個分であることと0.1と[MATH]\(\frac{1}{10}\)[/MATH]が等しいことから、0.8を[MATH]\(\frac{8}{10}\)[/MATH]と表せることや、分数を小数で表すときには、分子を分母で割ればよいことを、例えば[MATH]\(\frac{1}{2}\)[/MATH]を例にして指導しましょう。これらはとても重要な内容なので、全体交流でも押さえておくとよいでしょう。
机間巡視やタブレットの映像で、Bの方法で解いて活動を停止している子供を見付けたら、5年生で学習した小数の計算を使って計算していることを称賛したうえで、分数のかけ算に直すことにも取り組ませましょう。
Cの方法で解決した子供には、導いた答えが正しいことを図で確認するよう促しましょう。面積図による説明はやや難しいので、個別に指導していくというよりは、全体の学び合いの場面で確認するようにします。
全体の学び合いの場面では、まずBの小数に帰着する方法を取り上げます。0.8㎡の4等分は割り切れますが、3等分の場合、小数では正確に表せません。このことは、第5学年の分数と小数の混じった加法や減法の学習でも経験しています。
ここでも、「割り切れるときはよいけど、ほかの数だった場合は求められないのではないか」という子供の気付きをできれば取り上げながら、分数×分数で考えているCの考えへとつなぎます。Bの考えも生かしながらCの考えへと深めていきます。
まず、図で問題場面を確認し、図のどの部分が「0.8」「[MATH]\(\frac{1}{4}\)[/MATH]」なのかを伝え合い、理解できるようにします。
また、形式的な計算にとどまらず、答えが正しいことを図と関連して説明することで、答えが0.2㎡で正しいこととともに、根拠を明確にしながら筋道を立てて考えることにつながります。
ノート例
B 素朴に解いている子

C ねらい通りに解いている子

全体発表とそれぞれの考えの関連付け
問題②にはいろいろな数値があります。図で確認していきましょう。
イラスト/横井智美

