小4算数「分数をくわしく調べよう」指導アイデア
執筆／福岡県公立小学校教諭・太田佳奈
編集委員／文部科学省教科調査官・笠井健一、福岡教育大学教授・清水紀宏
目次
本時のねらい（本時3／９時）
数を構成する単位に着目し、ます図などの表現を基に分数を帯分数に直す方法を考え、説明することができる。
評価規準
除法を用いて、仮分数を帯分数や整数に直すことができる。また、除法の商とあまりが帯分数の整数部分と端数部分に当たることを説明することができる。（知識・技能、思考・判断・表現）
問題
[MATH]\(\frac{9}{4}\)[/MATH]と2[MATH]\(\frac{2}{4}\)[/MATH]は、どちらが大きいですか。
※帯分数どうしの大きさの比較のしかたをふり返り、 本時につなげる。
では、[MATH]\(\frac{9}{4}\)[/MATH]と2[MATH]\(\frac{2}{4}\)[/MATH]は、どちらが大きいですか。
仮分数と帯分数だから、比べられません。
どうすれば比べられそうですか。
昨日は帯分数どうしで比べたから、仮分数を帯分数に直すといいです。
学習のねらい
仮分数を帯分数に直す方法を考えよう。
見通し
- [MATH]\(\frac{1}{4}\)[/MATH]のいくつ分かで考える。
- ます図に表す。
- 数直線に表す。
自力解決の様子
A つまずいている子
分数を図や数直線に表すことができていない。
Ｂ 素朴に解いている子
図や数直線を用いて仮分数を帯分数に直している。
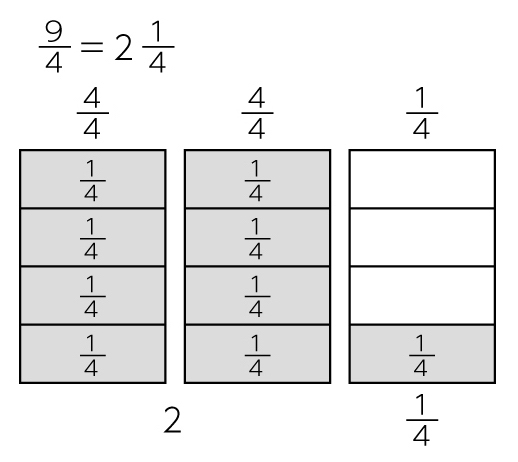
Ｃ ねらい通り解いている子
9÷4＝2あまり1という式を用いて、仮分数を帯分数に直すことができている。
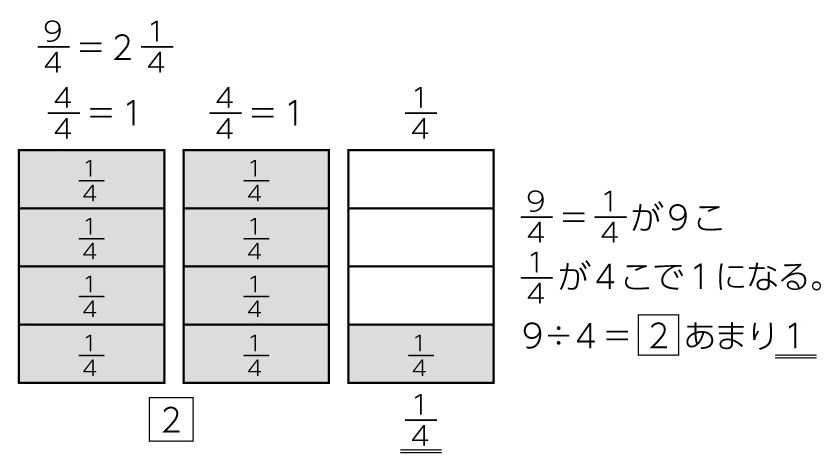
自力解決では、子供一人一人が自分に合った思考の道具（図や数直線、式など）を選び、仮分数を帯分数に直すことができるようにします。Aの子供には、前時をふり返らせ、分母の数に注目して、ます図をかくよう促します。Bの子供には、図や数直線を使い、視覚的に分かりやすくしていることを称賛したうえで、図や数直線をかかずに式に直す方法を考えるように促します。
学び合いの計画
イラスト／横井智美
『教育技術 小三小四』2022年2/3月号より
