小1算数「かたちづくり」指導アイデア(2/5時)《3枚の色板で基本図形を構成》

執筆/埼玉県入間市立金子小学校教諭・斉藤雄佑
監修/文部科学省教科調査官・笠井健一、浦和大学教授・矢部一夫

目次
単元の展開
第1時 直角二等辺三角形の色板を使って、いろいろな形を構成する。
▼
第2時(本時)3枚の色板で基本図形を構成する。
▼
第3時 決められた枚数の色板で、いろいろな形をつくる。
▼
第4時 数え棒を並べて、いろいろな形をつくる。
▼
第5時 格子点を直線で結んで、いろいろな形をかく。
本時のねらい
図形の特徴についての理解を深める。
評価規準
色板の形に着目し、色板をずらしたり回したり裏返したりすることを通して、いろいろな形を構成、分解することを考え、説明している。(思考・判断・表現)
本時の展開
前の時間は色板を使って、いろいろな形をつくりました。たくさんの形ができましたね。みんなのつくった形を見て不思議に思ったのですが、この二つは同じ形と言えますか。
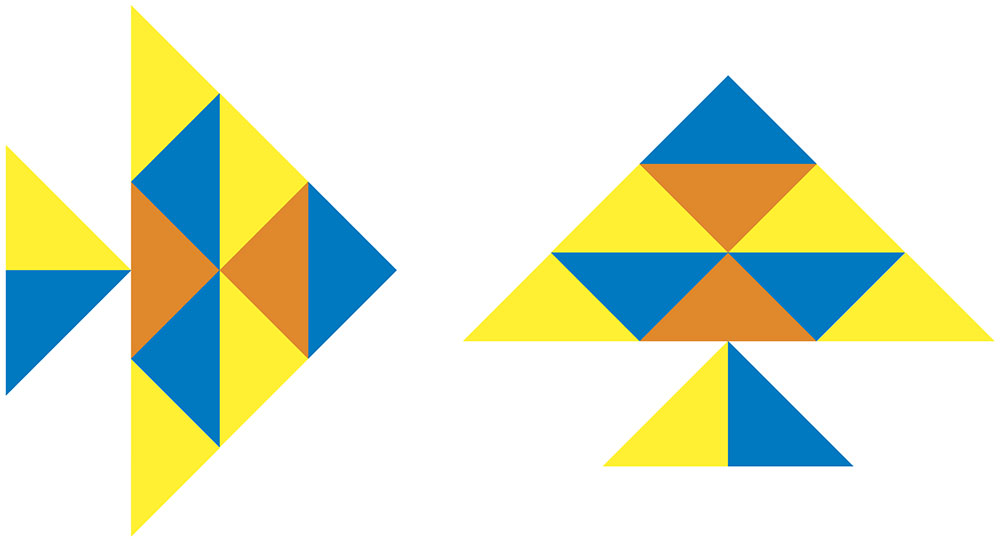
2つとも金魚のような形だから同じです。
向きを変えると同じ形になりました。向きが変わっただけなので、形は同じだと思います。
なるほど。向きが変わっただけですね。では、この三つの形は同じ形ですか、違う形ですか。
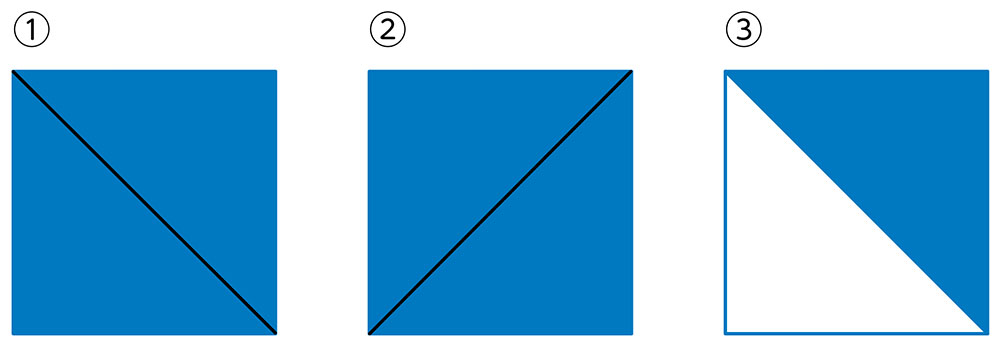
①と②は向きを変えれば同じです。
③は色が変わっているだけで、形は同じです。
色板の色や向きは関係なくて、周りの線で形は決まるのですね。

□まいの いろいたを つかって いろいろな かたちを つくりましょう。
1枚だったら何種類の形ができますか。
1枚だけでは、どうしても1種類しかできません。
そうですね。では、2枚だったらどうでしょう。
この3つです。

では、3枚だったらどうでしょう。
やってみないと分からないなあ。

3枚の色板で、何種類の形ができるか考えよう。
見通し
たくさんつくってみて、できた形が同じかどうか確かめてみよう。
2枚でできた形にもう1枚つなげていくとできそう。
まず3枚で形をつくって、そのあと1枚ずつ動かしてつくれないかな。
自力解決の様子
A つまずいている子
- 形はつくれるが、同じ形を違う形と捉えてしまったり、違う形を同じ形と捉えてしまったりする。
B 素朴に解いている子
- 3枚を試行錯誤しながら、いろいろ組み合わせて形を構成している。
C ねらい通り解いている子
- はじめに2枚の場合を考え、その形に残りの1枚を組み合わせて形をつくっている。
- まずは3枚で形をつくり、その中の1枚の色板をいろいろ動かして新しい形をつくり出している。
学び合いの計画
3枚の色板をいろいろ組み合わせて形をつくる学習は、2枚の色板の場合に比べ、さまざまな形ができたり、別の何かに似た形が偶然できたりするなどの楽しさがあります。しかし、それだけでは「かたちあそび」となってしまいます。
そこで、「3枚の色板を使って何通りの形ができるか」という問題解決の場面を設定します。そうすることで、子供たちはできる形をイメージしながら形をつくったり、2枚の色板でできた形を基に、3枚目の色板を加えて形をつくったりするなど、数学的な見方を働かせて主体的に形を構成することができます。
そのためにはまず導入段階で、教師がルールを明確にすることが重要です。例えば、辺と辺どうしを付けることや、色板を重ねてはいけないことをしっかり押さえることが大切です。自力解決中にルールを追加することがないよう、明確にしておきましょう。
また、「ものの形を認める」活動を重視します。「形」というのは、図形どうしをつなげたときにできる線や色は捨象し、辺だけを見るということを子供に気付かせます。
イラスト/横井智美

