小2算数「かけ算(3)」指導アイデア(3/6時)《簡単な場合の2位数と1位数の乗法》

執筆/東京都荒川区立第一日暮里小学校主幹教諭・石川大輔
監修/文部科学省教科調査官・笠井健一、東京都目黒区立八雲小学校校長・長谷豊

目次
単元の展開
第1時 九九表をつくり、九九表からさまざまなかけ算のきまりを見付ける。
▼
第2時 九九表から見付けたきまりを発表し合い、かけ算の掛ける数と積関係や交換法則、分配法則をまとめる。
▼
第3時(本時)簡単な場合の被乗数が2 位数のかけ算について、九九表を基に、学習してきたかけ算の性質やきまりを用いて答えの求め方を考える。
▼
第4時 九九を活用して、ものの数の求め方を、かけ算を用いて解決できるように工夫して考える。
▼
第5時 比較量を求めたり、図を見て基準量の何倍かを考えたりし、「倍」についての理解を深める。
▼
第6時 学習内容の定着を確認するとともに,数学的な見方・考え方をふり返る。
本時のねらい
数量の関係に着目して、簡単な場合の2位数と1位数の乗法の答えの求め方を、乗法の性質やきまりを基に考えることができる。
評価規準
簡単な場合の2位数と1位数の乗法の答えの求め方を、乗法の性質やきまりを基に考え、説明している。
本時の展開
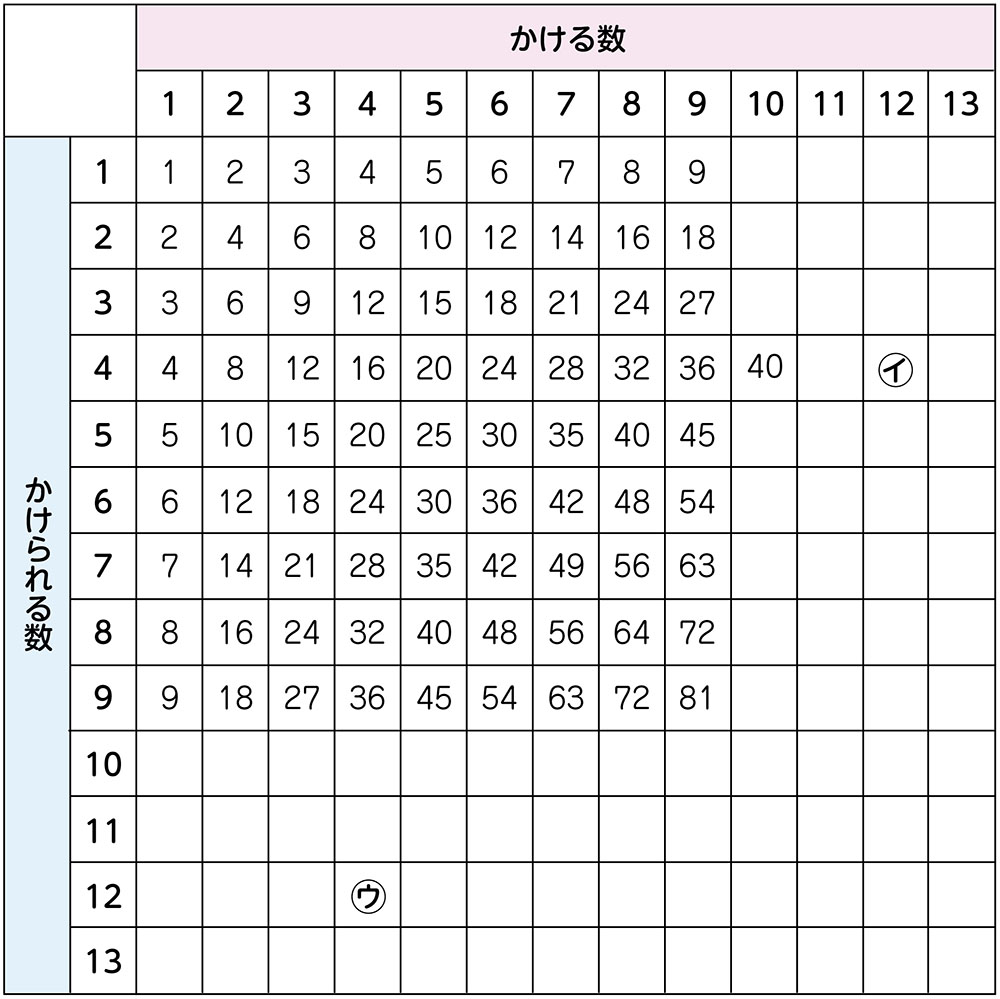
(表①を提示する)九九の復習です。唱えてみましょう。
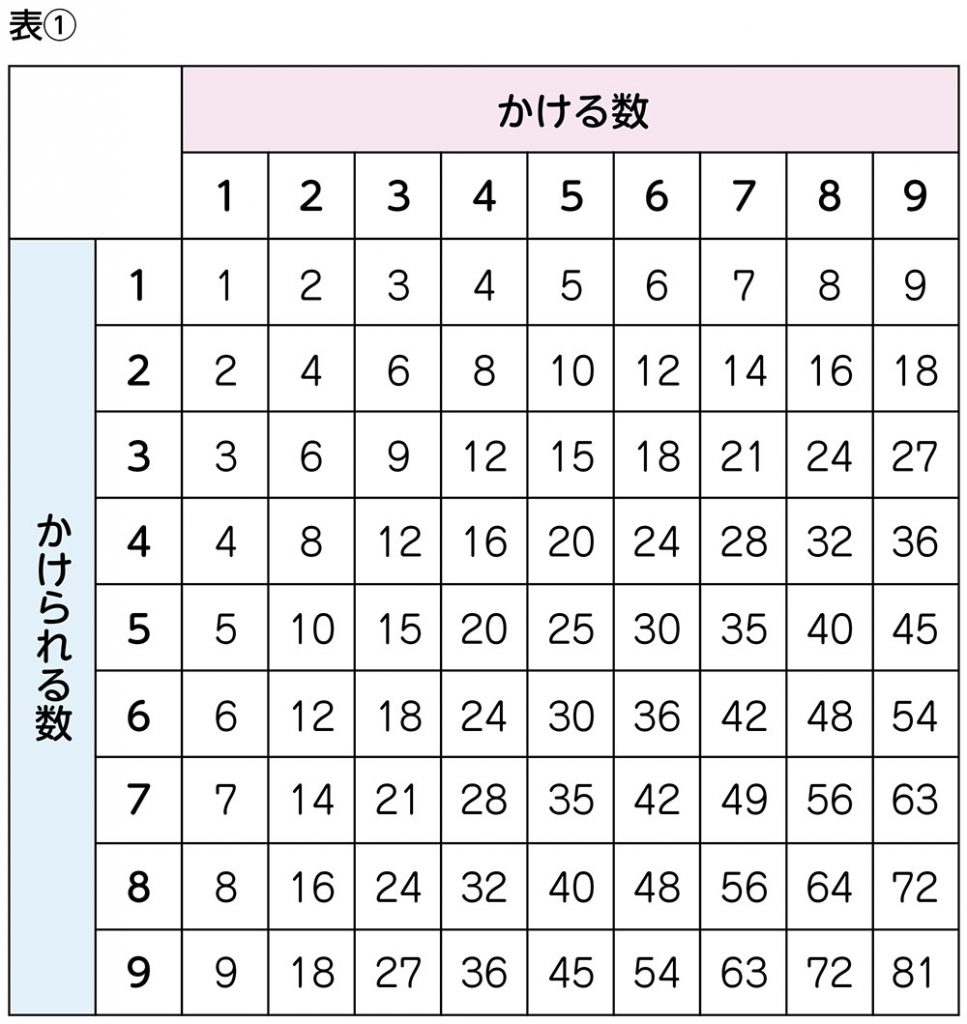
一一が1、一二が2、一三が3、……一九が9。二一が2、……九八72、九九81。簡単です。
よくできましたね。では、(表①を横と縦に広げて表②の形にする)㋐、㋑、㋒に入る数は、いくつでしょう。
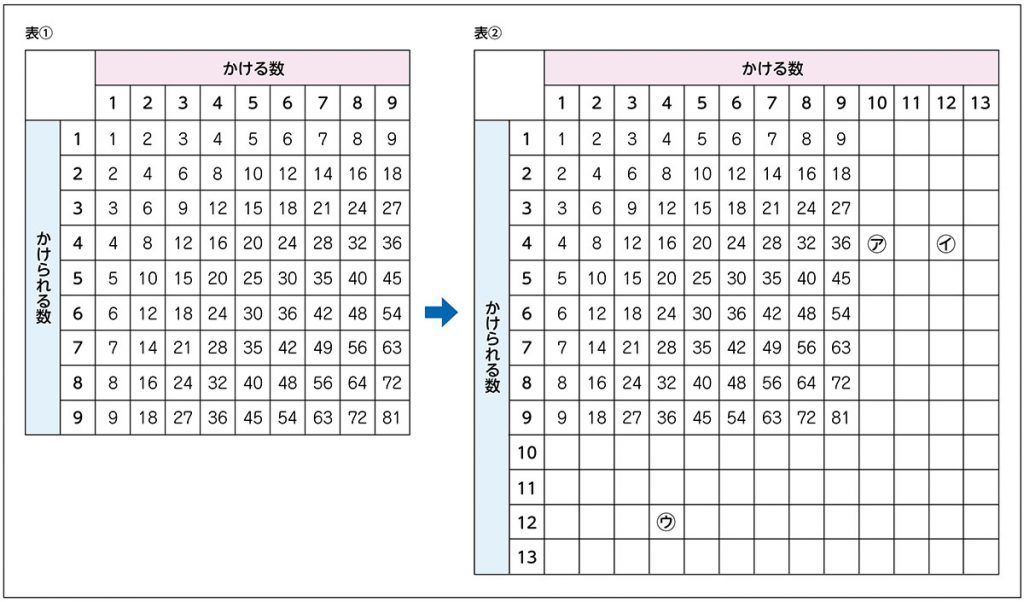

㋐、㋑、㋒に入る数はいくつでしょう。
えっ、九九表からはみ出ているよ。
㋐と㋑は4の段の続きだから……。
㋒は12の段? いくつか、分からないよ。
㋐、㋑、㋒に入る数を求める式は何でしょう。
㋐は、4×10です。
㋑は、4×12です。
㋒は、12×4です。
では、㋐、㋑、㋒に入る数が分かりますか。
どれも、九九にない式だから分かりません。
どうやって考えたら、答えが求められるかな。
㋐、㋑、㋒の式は、どれも九九にはありませんね。このような場合、どのように考えれば、答えが求められるでしょう。

九九よりも大きいかけ算の答えの求め方を考えよう。
見通し
一番答えが求められそうなのは、㋐、㋑、㋒のうち、どれですか。
㋐の4×10です。

最も答えが求められそうな式として、㋐の4×10が挙げられることが予想されます。この4×10の解き方から、既習の乗法の性質や乗法の意味、交換法則など、既習のかけ算のきまりを基に考えればよいことを押さえます。
※本時の学習を深めるためには、前時までにかけ算のきまりを知識・技能として習得しておくことが重要です。
答えは、いくつになりましたか。
40です。
どのように答えを求めたか、説明してください。
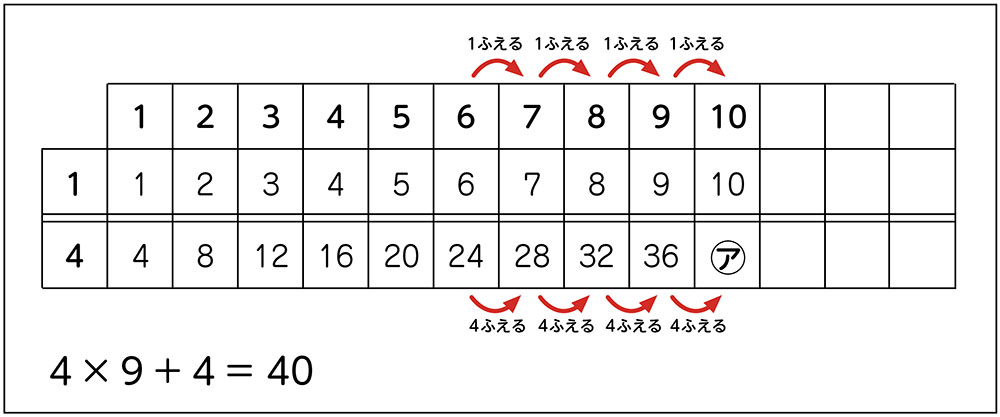
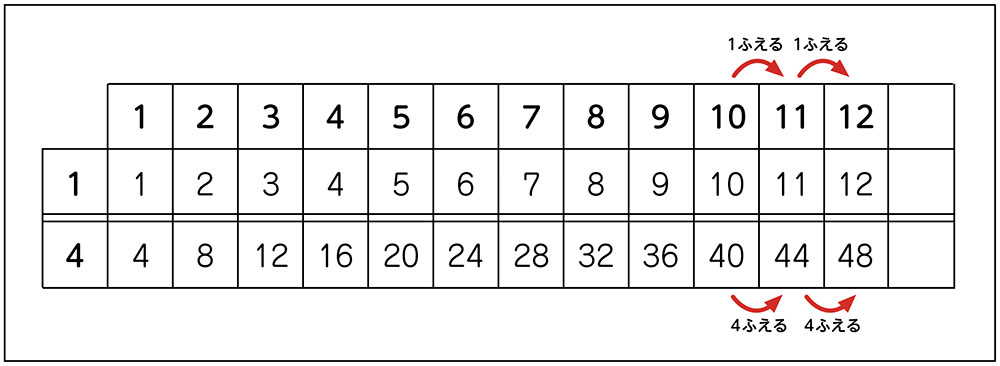
4の段は、かける数が1増えると、答えが4増えるから、4×9に4を足しました。
私は、4×10は4が10個分だから、4を10回足しました。
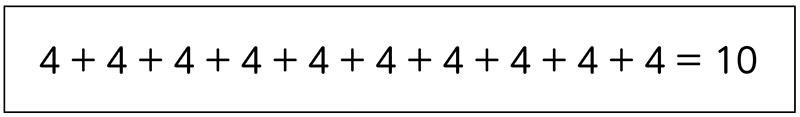
今まで学習したかけ算のきまりを使うと、計算できそうですね。では、㋑と㋒についても答えの求め方を考えてみましょう。考えた求め方は、九九表やノートに書きましょう。
※表②の形になった九九表を、紙、もしくはタブレットPCで配付する。考えは、この九九表やノートに書かせる。
自力解決の様子
A つまずいている子
九九を暗唱できなかったり、かけ算のきまりを理解していなかったりして、答えやその求め方を表やノートに書いていない。
どう考えたら、㋑や㋒の数を求められるのか分からないなぁ……。
B 素朴に解いている子
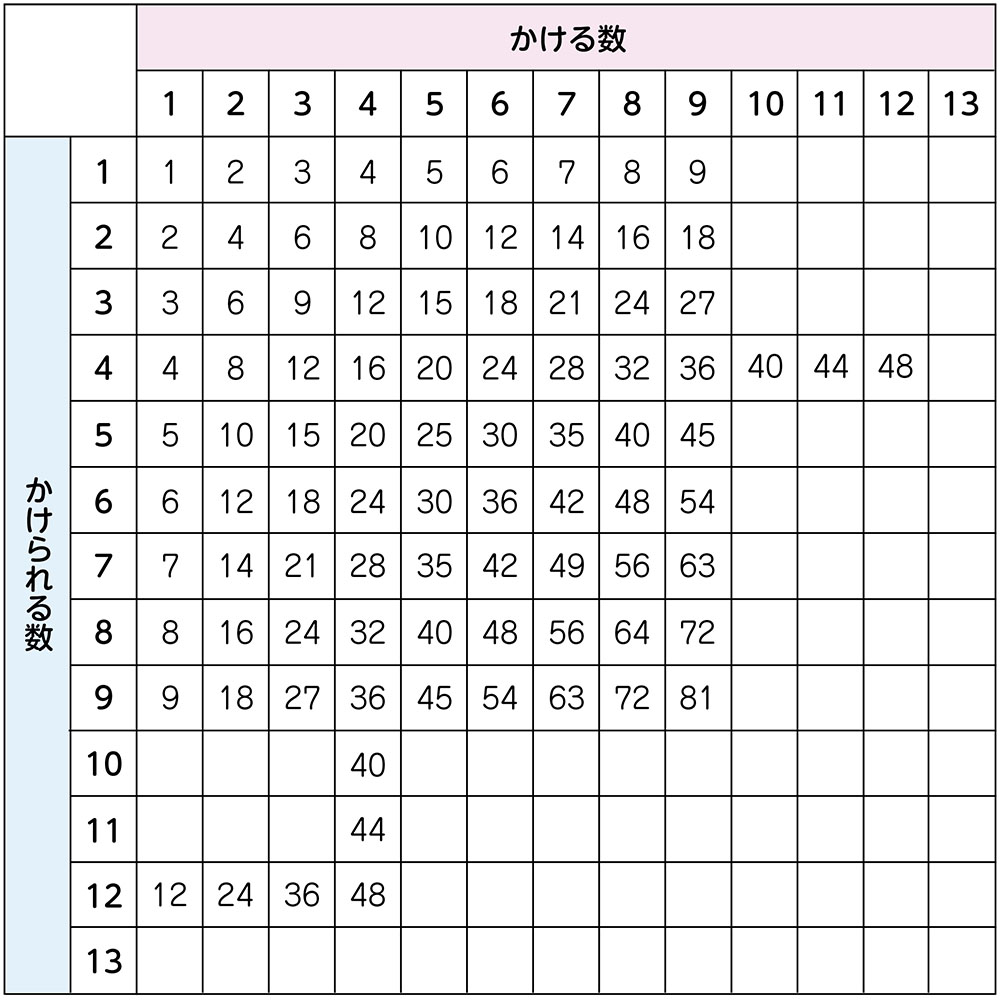
九九表を用いて答えを求めているが、かけ算の性質や意味、交換法則を根拠にした答えの求め方の説明が書けていない。
九九表に数を書いて考えてみよう。㋑は48で、㋒も48だ。
C ねらい通り解いている子
九九表や式、言葉を関連させて、かけ算の性質や意味、交換法則を根拠にした答えの求め方の説明と答えが書けている。
[㋑かける数と答えのきまり]4の段は、かける数が1増えると答えが4増えるから、4×12の答えは48だ。
[㋒同じ答えのきまり]12×4と4×12の答えと同じだから、12×4の答えは48だ。
学び合いの計画
自力解決ではAからCの子供のように、答えが求められない子供や根拠をもって多様に考えられる子供が存在します。このような子供たちがそれぞれ根拠を明確にもって説明できるように、全体の話合いの前にペアやトリオで説明し合う場を設定したり、全体検討である子供が説明したことを再現させたりします。
イラスト/横井智美

