小4算数「変わり方」指導アイデア《伴って変わる2つの数量の関係|和が一定》
執筆/富山県高岡市立博労小学校教諭・神田将義
監修/文部科学省教科調査官・笠井健一、前・富山県南砺市立福光東部小学校校長・中川愼一

目次
単元の展開
第1時(本時)伴って変わる2つの数量の関係(和が一定)について、表を用いてその関係を捉え、□や△を使って式に表す方法を考える。(□+△=9)
▼
第2時 伴って変わる2つの数量の関係(差が一定)について、表を用いてその関係を捉え、□や△を使って式に表す方法を考える。(□+2=△)
▼
第3時 伴って変わる2つの数量の関係(商が一定)について、表を用いてその関係を捉え、□や△を使って式に表す方法を考える。(□×4=△)
▼
第4時 問題に取り組み、学習内容の定着を確認し、理解を確実にする。
本時のねらい
伴って変わる2つの数量の関係を、表に整理して、□や△を使って式に表し、変化や対応の特徴を考える。
評価規準
伴って変わる2つの数量を見いだし、その関係を表や□や△を使った式に表して、変化や対応の特徴を考えている。(思考・判断・表現力)
本時の展開

同じ長さのストロー18本を使って長方形をつくります。どんな長方形をつくることができるでしょうか。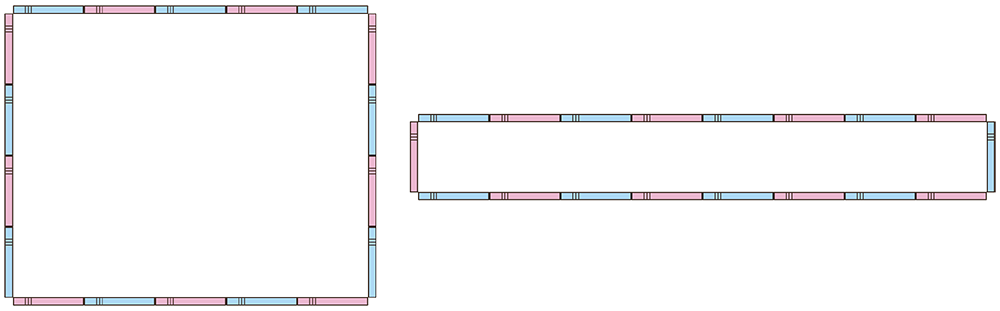
ドットシートを使って、どんな長方形をつくることができるのか調べていきましょう。

こんな細長い長方形ができました。
「こんな細長い」を「縦」や「横」などの算数の言葉を使って言い表すことはできますか。
縦がストロー2本で、横がストロー7本の長方形です。
「縦2、横7」と言えば簡単に表せるよ。
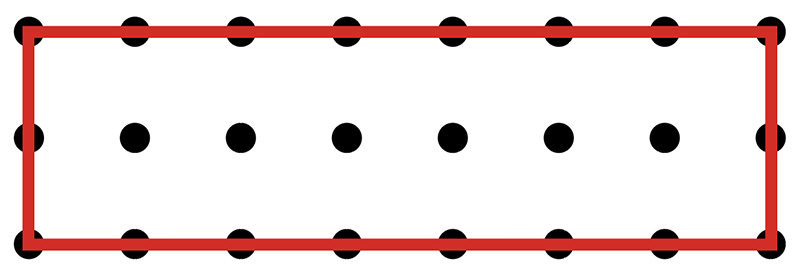
皆さん、今の表し方でよいですか。それでは、ほかにできる長方形も「縦○、横□」で表してみましょう。
私がつくった長方形は、「縦5、横4」です。
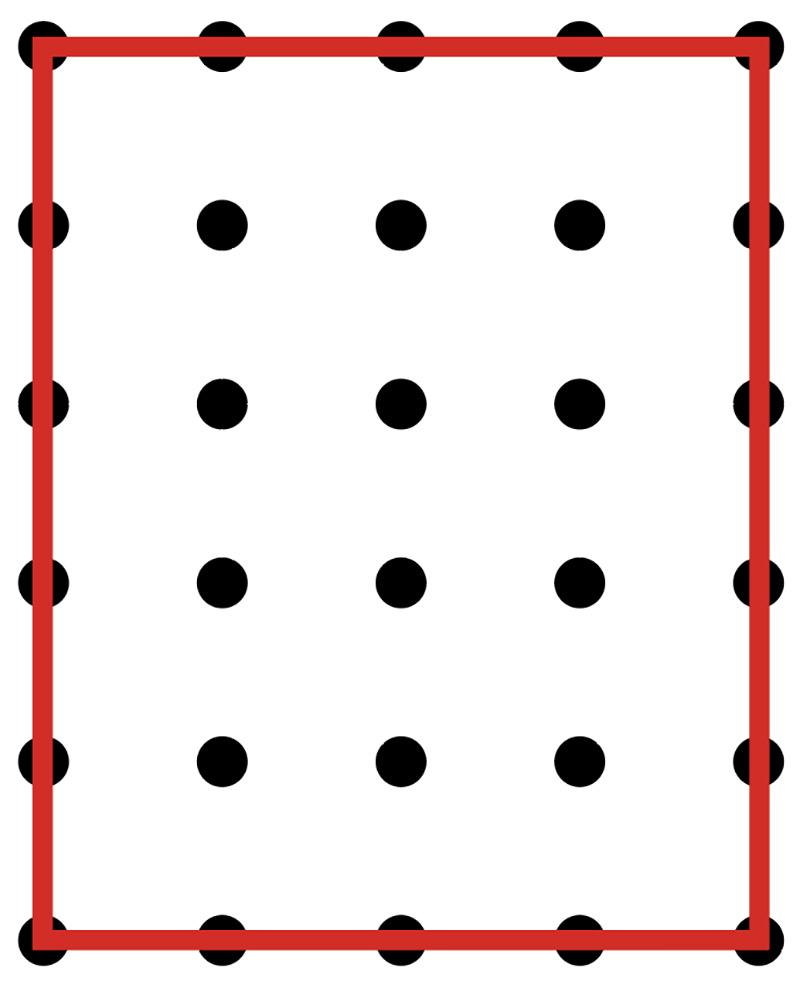
僕は「縦1、横8」です。

いちいち書いて調べなくても、縦の数が分かれば横の数も分かりそうです。
それは、どういうことですか。
縦と横を足したら9になるというきまりがあるみたいだからです。
では、ほかの長方形も調べてみましょう。たとえば、縦が3のとき、横の数はいくつですか。
6だと思います。
本当だ。ドットシートにかいて確かめてみたら、6になっています。
そのきまりがすべての場合にあてはまるのか、調べていきましょう。

長方形の縦の数と横の数にあるきまりをはっきりさせよう。
見通し
長方形の縦の数と横の数の組合せを全部調べていけばきまりが見付かりそうだ。(方法の見通し)
たくさんの組合せがあるので、縦の数と横の数の組合せを順に並べていけば、見やすくなりそう。(方法の見通し)
縦の数と横の数を足したら9になるというきまりがありそうだ。(結果の見通し)
自力解決の様子
A つまずいている子
「縦の数が2のとき、横の数は7」
・長方形をドットシートにかき出して調べているが、きまりに気付けず困っている。
B 素朴に解いている子
「縦の数と横の数を足したら9になりそう」
・2~3通りの具体から、直感的にきまりを考えている。
C ねらい通り解いている子
「縦の数と横の数の和を順に調べたら、どの組合せも和が9になっている」
・縦の数と横の数を順に表に整理して、和が一定であることを見いだしている。
学び合いの計画
ここでは、2つの数量の関係を表に整理し、その表を読み取ることで2つの数量の関係の特徴を見いだすことを大切にして学習を進めます。
イラスト/横井智美、やひろきよみ

