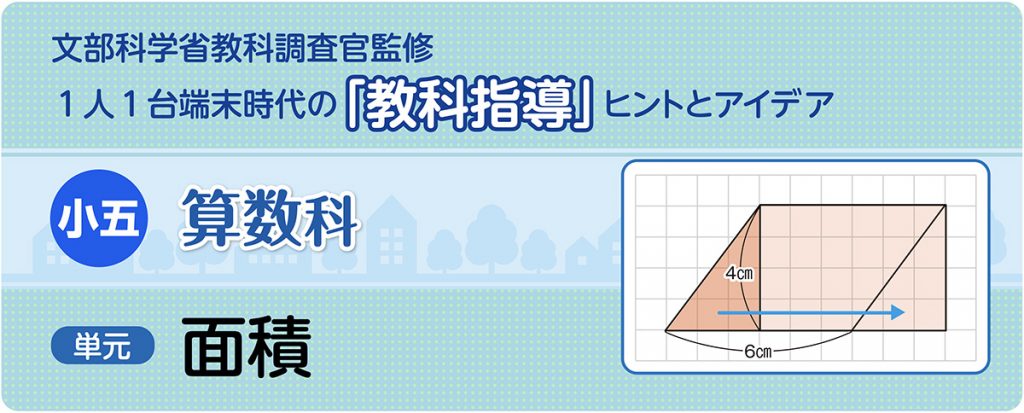
小5算数「面積」指導アイデア《平行四辺形の面積の求め方》
執筆/福岡県北九州市立中原小学校教諭・中村真弥
監修/文部科学省教科調査官・笠井健一、福岡教育大学教授・清水紀宏

目次
単元の展開
第1時(本時)平行四辺形の面積の求め方を考え、説明することができる。
▼
第2時 平行四辺形の面積の公式をつくり出し、それを適用して面積を求めることができる。
▼
第3時 高さが平行四辺形の外にある場合でも、平行四辺形の面積の公式を適用できることを理解する。
▼
第4時 三角形の面積の求め方を考え、説明することができる。
▼
第5時 三角形の面積の公式をつくり出し、それを適用して面積を求めることができる。
▼
第6時 高さが三角形の外にある場合でも、平行四辺形の面積の公式を適用できることを理解する。
▼
第7時 台形の面積の求め方を考え、説明することができる。
▼
第8時 台形の面積の公式をつくり出し、それを適用して面積を求めることができる。
▼
第9時 ひし形の面積の求め方を考え、説明することができる。また、ひし形の面積の公式をつくり出し、それを適用して面積を求めることができる。
▼
第10時 学習の定着を確認する。
本時のねらい
既習の図形に帰着して、平行四辺形の面積の求め方を考える。
評価規準
長方形に変形して、平行四辺形の面積を求めることができる。(思考・判断・表現)
1人1台端末活用ポイント
本単元では、単元を通してタブレット端末(以下、「タブレット」)を用いながら面積公式を作りだす活動を設定します。
タブレット上では、図形のどの長さに着目すれば面積を求めることができるか説明できるように、等積変形や倍積変形をした後の図形だけでなく、最初の図形についても説明に合わせて表示できるようにします。
本時では、平行四辺形の隣り合う2つの辺の長さを掛けて面積を求める考えや、平行四辺形を「切って組み合わせる」(「裁ち合わせ」と言います。以下は、単に「変形して」とします)ことで、長方形に変形する考えを取りあげて、平行四辺形の面積の求め方を話し合わせます。
そのために、縦5㎝、横6㎝の長方形の4つの辺の長さを変えずに、2つの頂点の位置を変えてつくった平行四辺形を提示し、面積を尋ねます。
本時の展開

㋐の長方形の辺の長さを変えずに、㋑の平行四辺形にしました。㋑の面積は何㎠ですか。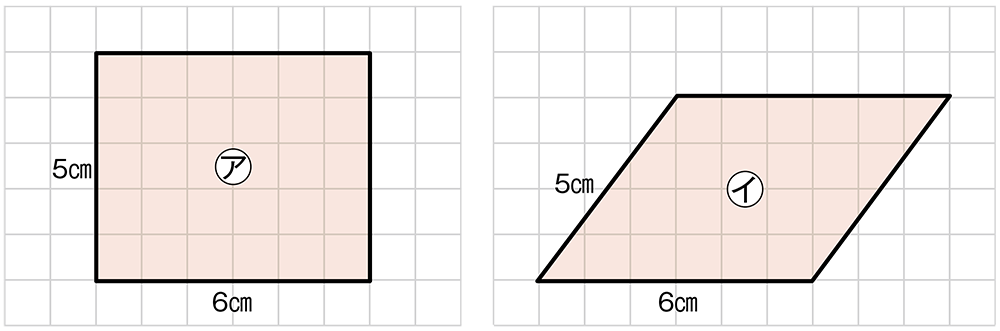
導入では、既習の㋐の図形について求積のしかたを全体で確認します。次に、頂点の移動の様子が分かるように、ICT環境を使って図形を動的に映し出し、図形が変わったときの面積の求め方について話し合わせます。
(問題を掲示)㋐の面積を求めることはできますか。四年生で学習しましたね。
縦×横をすればすぐに答えが出せます。
5×6で30㎠になります。
この「5×6」とは、何が5×6個あるのですか。
1㎠の正方形が5×6個あります。
では、上の辺を動かします(タブレット上で図形の変化を映す)。四角形の面積はどうなったでしょう。
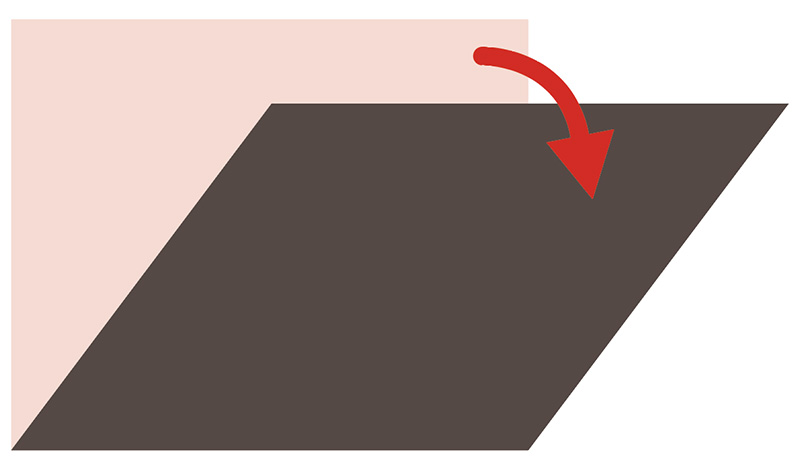
小さくなった!
(子供のつぶやき)大きくなったように見えたけど……。
図形のどこの部分が変わりましたか。
縦の線が斜めになりました。
右に倒れて平行四辺形になりました。
直角がなくなりました。
辺の向きや角度が変わったようですが、長方形の面積を求める考え方はもう使えないのでしょうか。
同じ四角形だから、縦×横が使えると思います。
四年生のときみたいに、ます目の数を数えたら分かると思います。
そのままだと、斜めの辺があって数えられません。
正方形の数が数えられるように、平行四辺形を切ったり動かしたりすればよいかな。
なるほど。さまざまな方法があるようですね。今日はいろいろな方法で平行四辺形の面積の求め方を考えて、それを説明するというめあてでよいですか。

平行四辺形の面積を求める方法を考えて説明しよう。
タブレットのアプリで図形を切ったり動かしたりすることができます。この図形を方眼紙にかいたものも配ります。アプリと方眼紙の好きなほうを使って考えましょう。答えだけでなく、言葉の説明も書き加えて、面積を求める方法を説明しましょう。
※この指導アイデアでは、タブレット上で図形を切ったり動かしたりする操作が可能な学習アプリを使用することを想定しています。このようなアプリを使用しない(できない)場合は、方眼紙を使った活動を位置付けて授業を展開していきます。
自力解決の様子
子供のタブレットの画面上に平行四辺形を映すとともに、同じ図形が方眼紙にかかれたノート用の紙を4枚程度、子供に配付します。タブレットを使用するか、方眼紙を使用するかは、子供に選択させます。図形を切ったり動かしたりして、まずは、自由に操作をさせながら面積を考えさせます。
次に、どのように考えたのか、学級全体に向けて説明ができるように、自分が操作した手順や考え方を、図形に文字や記号などを使ってタブレットに書き込ませます。書き終わったら、教師のタブレットに提出させて、学び合いの準備をします。
なお、全体で交流させたい考えが浮かんでいても、タブレット上での操作がうまくいかない子供には、黒板に掲示できる図形を拡大した紙を渡し、切ったり書き込んだりさせます。
自分の考えがまとまったら、近くの友達どうしやICTの活用でほかの子供の活動を共有することも考えられます。このことによって、5×6という考えと、4×6という考えのどちらが正しいかを明確にするという新たなめあてが生まれるかもしれません。
また、面積は「1㎠の何個分」で表されるという測定の考えに基づき、面積を素朴に求める方法を確認できたり、三角形を長方形に変形する方法が多様にあることに触れることができたりします。これらはどれも本時の学習では大切な視点です。
ただし、子供たちがどの考えを参照するかはそれぞれの子供によってまちまちなので、全体の交流で順に取り上げていくとよいでしょう。
A つまずいている子
横の辺に対して垂直になっていない斜めの辺を「縦」と見て、長方形と同じ公式を使って計算している。
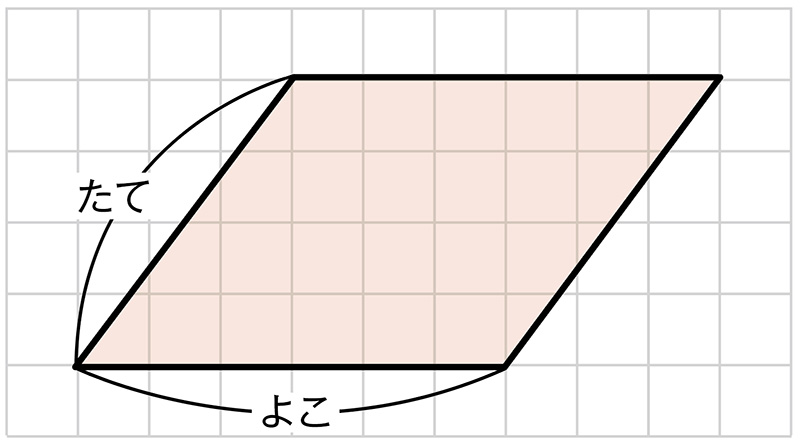
5×6=30 30㎠
B 素朴に解いている子
ます目の数を数えて求めている。
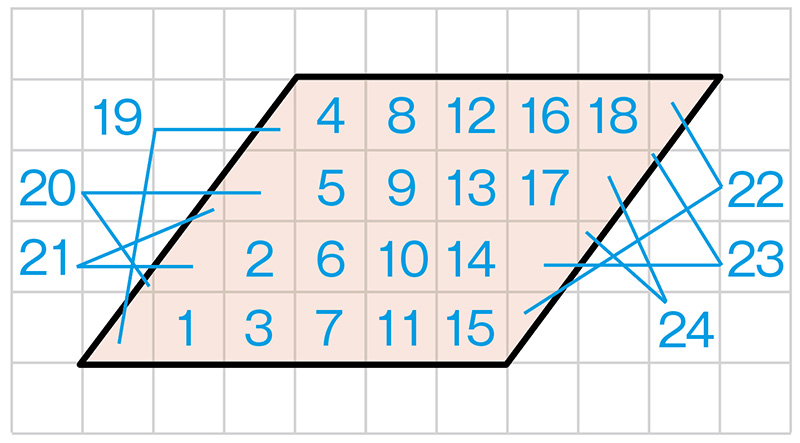
24㎠
C ねらい通り解いている子
- 垂直方向の線を引いて切り取り、動かして長方形をつくり、長方形の面積を公式で求める。

4×6=24 24㎠
- 垂直方向の線を2本引いて三角形2つと正方形に分け、三角形2つを組み合わせて長方形をつくり、それぞれの面積を求めている。
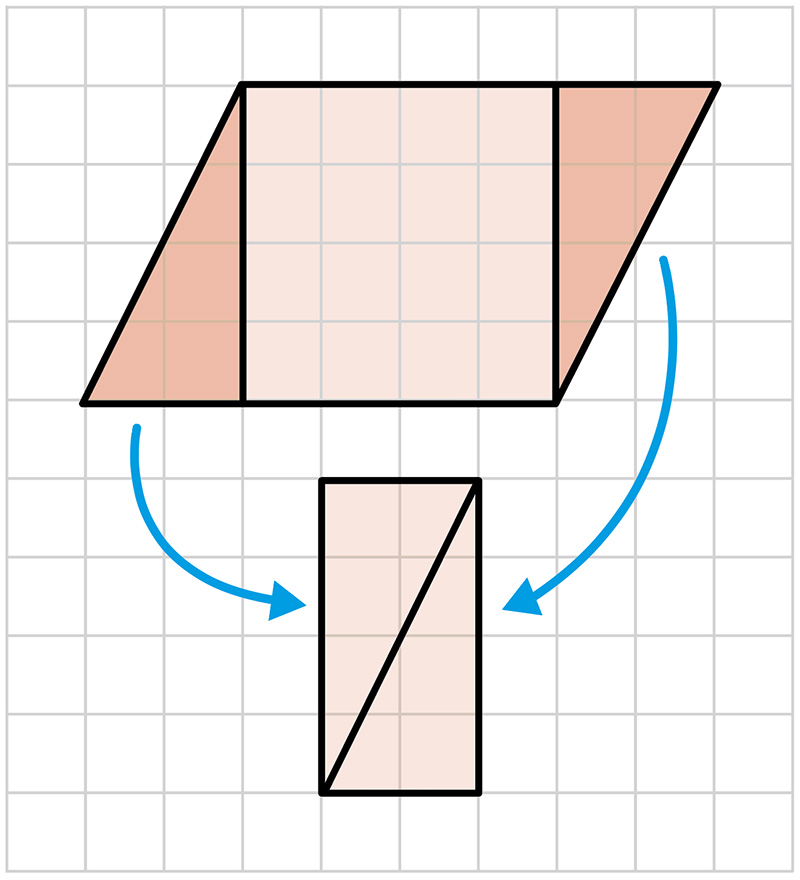
4×4+4×2=24 24㎠
- 水平方向の線を3本引き、4つの部分に分けた後、図のような長方形に変形し、その面積を求めている。
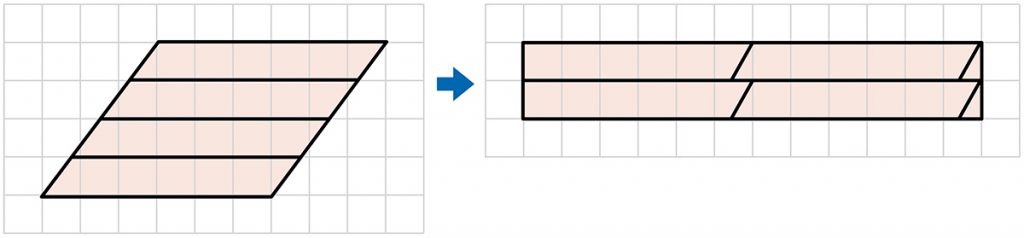
2×12=24 24㎠
ノート例
イラスト/横井智美

