小5算数「分数と小数、整数」指導アイデア《整数の除法の結果を分数で表す》

特集: 文部科学省教科調査官監修｢教科指導のヒントとアイデア｣

2022.09.15

単元の展開

第１時（本時）分数の意味に着目し、整数の除法の結果を分数で表す方法を考える。
▼
第２時　商分数の適用問題
▼
第３時　整数倍や小数倍の分数倍の意味を基に、分数倍の意味について考える。
▼
第４時　分数の意味に着目し、分数を小数や整数で表す方法を考える。
▼
第５時　小数や整数の意味に着目し、小数や整数を分数で表す方法を考える。

本時のねらい

分数の意味に着目し、整数の除法の結果を分数で表す方法を考える。

評価規準

（整数）÷（整数）を図と関連付けながら、その商を分数で表すことができる。

本時の展開

ジュース２Ｌを□人で等しく分けます。１人分は何Ｌになりますか。
※□に入れる数字を教師が２→４→３とする。

□を２にします。２人で等しく分けるとき、１人分は何Ｌになりますか。

１人分は１Ｌです。

今の答えを式と一緒に言えますか。

式は２÷２＝１で、１人分は１Ｌです。

そうですね。では、□を４にしてみます。２Ｌを４人で等しく分けるとき、１人分は何Ｌになりますか。

２÷４＝０.５なので、１人分は０.５Ｌです。

２÷４で正しいですか。４÷２ではないですか。

４等分なので、÷２ではなくて、÷４だと思います。

そうですね。では、□を３にします。３人で等しく分けるときは、１人分を求める式はどうなりますか。

２÷３です。

１人分は何Lでしょうか。計算してみましょう。

計算したら、0.66……となります。割り切れません。

１人分は0.6Ｌで、あまりは0.2Ｌです。

なるほど。でも、等しく分けたいので、あまりは出ないようにしたいですね。例えば、同じ３等分でも１Ｌを３人で等分するとき、1人分は何Lと言ったらよいでしょうか。

やっぱり１÷３＝0.33……になって、割り切れません。

[MATH]\(\frac{1}{3}\)[/MATH]Ｌだと思います。

なるほど。分数を使ったんですね。では、今度は２Ｌの３等分を考えてみましょう。

割り切れないわり算の商の表し方を考えよう。

導入では、□に教師が意図的に数値を選んでいき、これまでのわり算が、商が整数となって割り切れる場合、商が小数となって割り切れる場合、あまりのある場合という、それぞれの場合をふり返り、本時では、割り切れない場合にあまりを出さずにどのように商を求めるのかを考えるというめあてへとつなげていきます。

２÷３が0.66……と割り切れないことを確認した後、「１Ｌの３等分」を提示します。この場合も割り切れないのですが、分数を使うと1人分が[MATH]\(\frac{1}{3}\)[/MATH]Ｌと表現できることを押さえ、後の探究の手がかりとします。

見通し

[MATH]\(\frac{1}{3}\)[/MATH]Ｌ
[MATH]\(\frac{2}{3}\)[/MATH]Ｌ
図を使って考える。

自力解決の様子

A つまずいている子

３等分なので[MATH]\(\frac{1}{3}\)[/MATH]Ｌと考える。

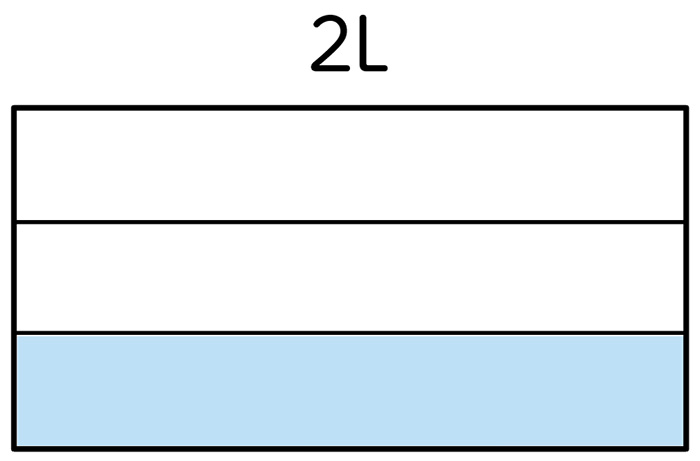
２Ｌを１つの長方形で表し、それを３等分している。

Ｂ素朴に解いている子

２Ｌを縦に分けた図や、下のように１Ｌずつ左右に２つ置いた図をかき、1人分を[MATH]\(\frac{2}{3}\)[/MATH]Ｌと捉えている。

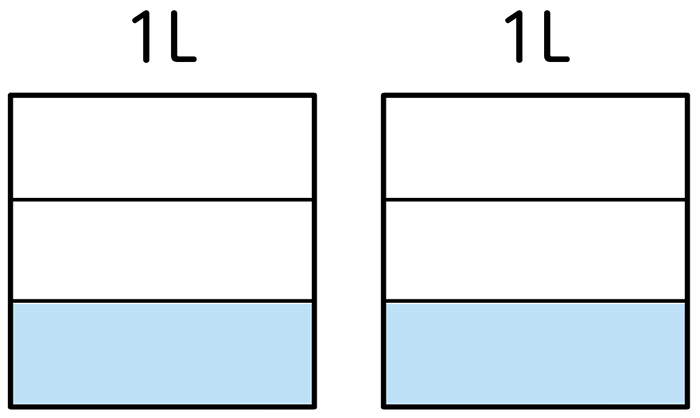
Ｃねらい通り解いている子

最初の立式と図による表現を関連付けて、２÷３＝[MATH]\(\frac{2}{3}\)[/MATH]であることを理解している。

学び合いの計画

Ａの子供は、分割分数（あるものの[MATH]\(\frac{1}{3}\)[/MATH]の大きさ、例えば、２Ｌの[MATH]\(\frac{1}{3}\)[/MATH]の大きさ）と、量分数（１Ｌの[MATH]\(\frac{1}{3}\)[/MATH]の大きさが[MATH]\(\frac{1}{3}\)[/MATH]Ｌ）を混同しています。

イラスト／横井智美

【関連記事】

文部科学省教科調査官監修｢教科指導のヒントとアイデア｣シリーズはこちら！