小4算数「小数のしくみ」指導アイデア《小数の大小関係を比較する方法》
執筆/富山県高岡市立能町小学校教諭・本間大輔
監修/文部科学省教科調査官・笠井健一、前・富山県南砺市立福光東部小学校校長・中川愼一

目次
単元の展開
第1時 十進構造の単位の構成に着目、[MATH]\(\frac{1}{100}\)[/MATH] の位までの小数の表し方
▼
第2時 十進構造の単位の構成に着目、[MATH]\(\frac{1}{1000}\)[/MATH] の位までの小数の表し方
▼
第3時 整数の仕組みからの類推、小数の構成や位取りの原理
▼
第4時(本時)十進位取り記数法に着目、小数の大小
▼
第5時 位の変わり方への着目、小数を10倍した数や[MATH]\(\frac{1}{10}\)[/MATH] にした数
▼
第6時 十進位取り記数法に着目、小数の相対的な大きさの表し方
▼
第7時 十進位取り記数法に着目、[MATH]\(\frac{1}{100}\)[/MATH] の位、[MATH]\(\frac{1}{1000}\)[/MATH] の位の小数のたし算の筆算のしかた
▼
第8時 十進位取り記数法に着目、[MATH]\(\frac{1}{100}\)[/MATH] の位、[MATH]\(\frac{1}{1000}\)[/MATH] の位の小数のたし算(小数の桁数が揃ってない場合)の筆算のしかた
▼
第9時 十進位取り記数法に着目、[MATH]\(\frac{1}{100}\)[/MATH] の位、[MATH]\(\frac{1}{1000}\)[/MATH] の位の小数のひき算の筆算
▼
第10時 十進位取り記数法に着目、[MATH]\(\frac{1}{100}\)[/MATH] の位、[MATH]\(\frac{1}{1000}\)[/MATH] の位の小数のひき算(小数の桁数が揃ってない場合)の筆算のしかた
▼
第11時 数の合成・分解や相対的な大きさの表し方に着目、小数の多様な見方
▼
第12時 学習内容の生活への活用
▼
第13時 学習内容の習熟や定着、数学的な見方・考え方のふり返り
本時のねらい
(整数の仕組みに着目し、小数の構成や位取りについて学習した後)
整数の大きさの比べ方を基にして、小数の大小関係を比較する方法を考える。
評価規準
整数の大きさの比べ方を基にして、小数の大小関係を比較する方法を考え、説明している。[思考・判断・表現]
本時の展開

㋐2.43と㋑2.47は、どちらの数が大きいでしょう。
この2つの小数では、どちらの数が大きいですか。
どちらも数字が3つあるから、桁の数では比べられなさそうです。
[MATH]\(\frac{1}{100}\)[/MATH] の位の3と7を比べると、7のほうが大きいので2.47のほうが大きいです。
どうして、3と7を比べたのですか。
その前の一の位の2も、[MATH]\(\frac{1}{10}\)[/MATH]の位の4も同じ数字だから、その次の数の3と7で比べました。
整数の大きさを比べるときは、上の位の数から順に比べたから、小数も同じように比べたらいいと思います。
小数の大きさ比べも、上の位から順番に比べたらできそうですね。位取り表に書いてみましょう。

位取り表に書くと、上の位から比べやすいな。
2.47のほうが大きいかどうか、数直線に表して確かめてみましょう。一番小さい1目盛りの大きさはいくつですか。
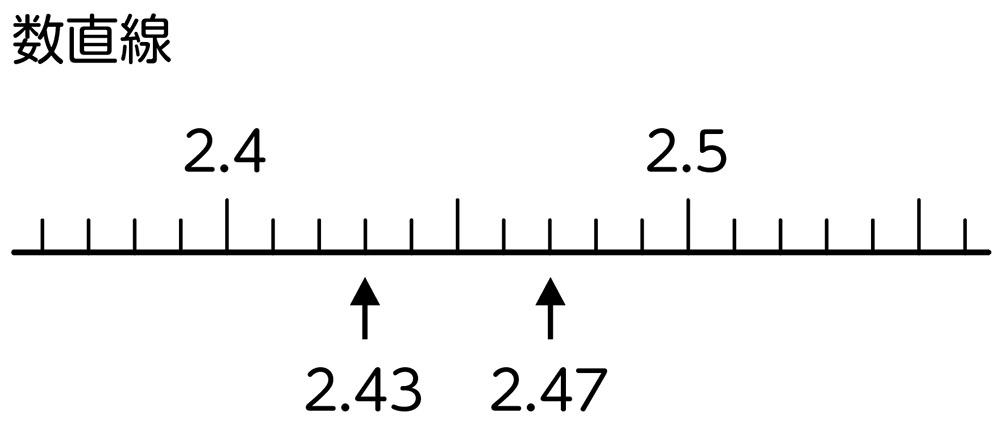
0.1を10個に分けているので0.01です。
やっぱり2.47のほうが大きいね。
それでは、この2つの小数はどちらが大きいでしょう。

㋑2.47と㋒2.458は、どちらの数が大きいでしょう。
桁の数が多いから、㋒のほうが大きそうだな。
整数のときは桁の数で比べられたけど、小数もそれで比べていいのかな。
それでは、どうやったら小数の大きさを比べられるのか、考えましょう。

小数の大きさのくらべ方を考えよう。
見通し
整数と同じように位取り表を用いて、上の位から順番に考えると比べられそうだ。〔方法の見通し〕
小数でも数直線に表してみると、ひと目で大きさを比べられそう。〔方法の見通し〕
自力解決の様子
A つまずいている子
- 桁の数が多いほうが大きいと考え、桁の数で比べている。
- それぞれの数の一番下の位で比べている。
B 図を使って解いている子
- 位取り表を用いて、上の位から順に比べている。
C ねらい通り解いている子
- 整数と同じように、上の位から順に比べたらよいことに気付いている。
- 整数とは違って、桁の数では比べられないことに気付いている。
学び合いの計画
この学習では、まず一つ目の学習問題(桁の数が等しい二つの小数の大きさ比べ)を考えることを通して、「小数も、整数と同じように上の位から順に比べると、大きさ比べができそうだ」との見通しをもたせます。その後に、二つ目の学習問題(桁の数が異なる二つの小数の大きさ比べ)を提示して考えさせることで、小数の場合は桁の数では比べることができないことや、整数と同じように上の位から順に比べたらよいことに気付けるよう展開するとよいでしょう。
イラスト/横井智美

