小2算数「2けたのたし算」指導アイデア《2位数+2位数の繰り上がりのある計算》
執筆/東京都立川市立幸小学校教諭・小泉 友
監修/文部科学省教科調査官・笠井健一、東京都目黒区立八雲小学校校長・長谷 豊
単元の展開
第1時 35+12の計算のしかたを考える。
▼
第2時 32+4の計算のしかたを考える。
▼
第3時(本時)35+29の計算のしかたを考える。
▼
第4時 2位数+2位数(繰り上がりあり)の筆算のしかたをまとめる。
▼
第5時 2位数+1、2位数=2位数(繰り上がりあり、答えの一の位に空位あり、欠位あり)の筆算のしかたを理解し、その計算ができる。
▼
第6時 加法について、交換法則が成り立つことを理解する。
▼
第7時 学習内容の定着を確認するとともに、数学的な見方・考え方をふり返る。
本時のねらい
2位数の繰り上がりのある計算について、前時までの筆算で働かせた位ごとの数の見方を活用して、計算のしかたや筆算のしかたを考えることができる。
式などの数学的表現を用いて考えた過程をふり返り、そのよさに気付き、生活や学習に活用しようとする。
評価規準
35+29の計算のしかたを数の見方(位ごとの数)を活用して、操作や図、式を用いて考え、説明している。

ひろしさんは35円のドーナツと2□円のグミを買います。だい金はいくらになりますか。
※問題場面を提示する。
先生、グミが何円なのか分かりません。
先生もグミがいくらだったのか、忘れてしまったのです。でも、21円か29円か、どちらかだったんですよ。
21円だったら簡単です。前にやった筆算でやればいいです。
21円だったらすぐにできるのですね。
29円でもできそうだけど……。
では、21円だったら、どうすれば答えを求めることができますか。
35+21でできます。
では、35+21は筆算を使えばできると言っていましたね。ノートに計算してみましょう。
できました。
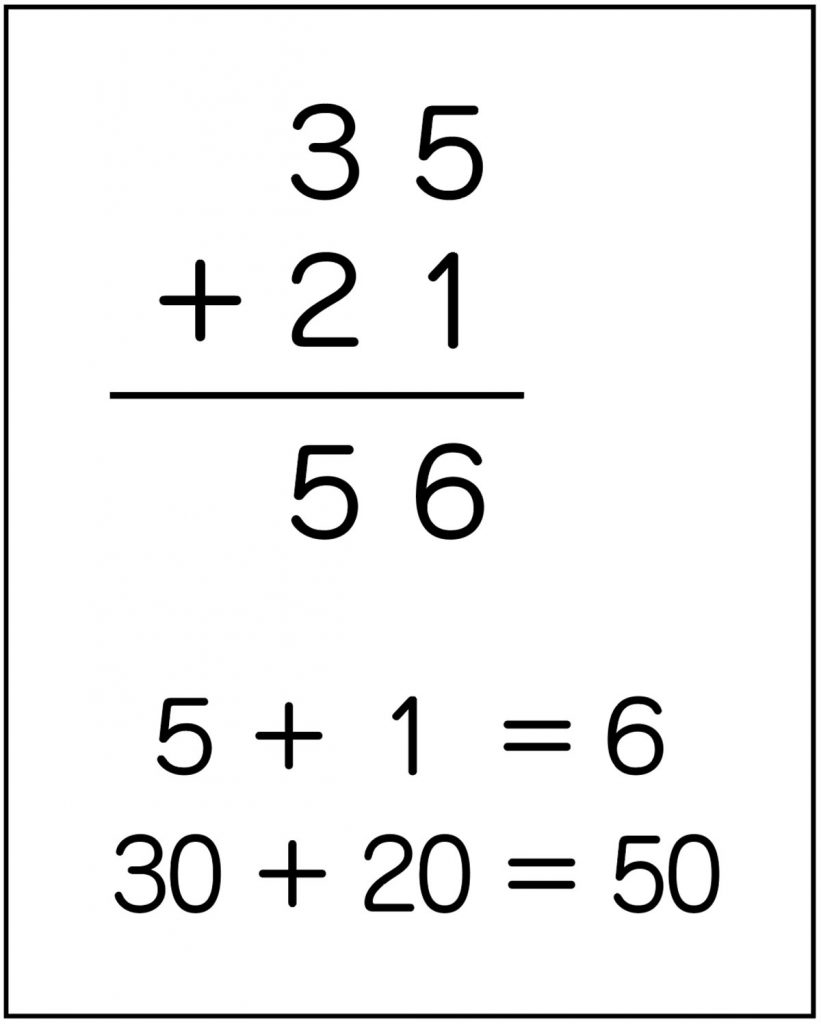
どうやって計算したのか、教えてください。
まず、一の位の5+1をして6。次に十の位の3+2をして56になります。
今の説明が、もう一度できる人はいますか。
※1人の発言で終わらず、解釈したことを伝え合ったり、発言を途中から発言させたりして、前時までのたし算の場面を確認する。
35+21は筆算でできましたね。では、29円のときはできますか。
できそうです。式は35+29になります。
でも、一の位を足すと10を超えてしまうよ。
35+29は35+21よりも難しいところがあるのですね。答えを求めることはできませんか。

35+29の計算の答えの求め方を考えよう。
見通し
どうすれば答えを求めることができそうですか。
筆算みたいに一の位から足せば、答えを求めることができそうです。
一の位と十の位を分けて計算すればいいです。
筆算でもできます。
自力解決の様子
A つまずいている子
筆算では書いているが、繰り上がりを忘れている。
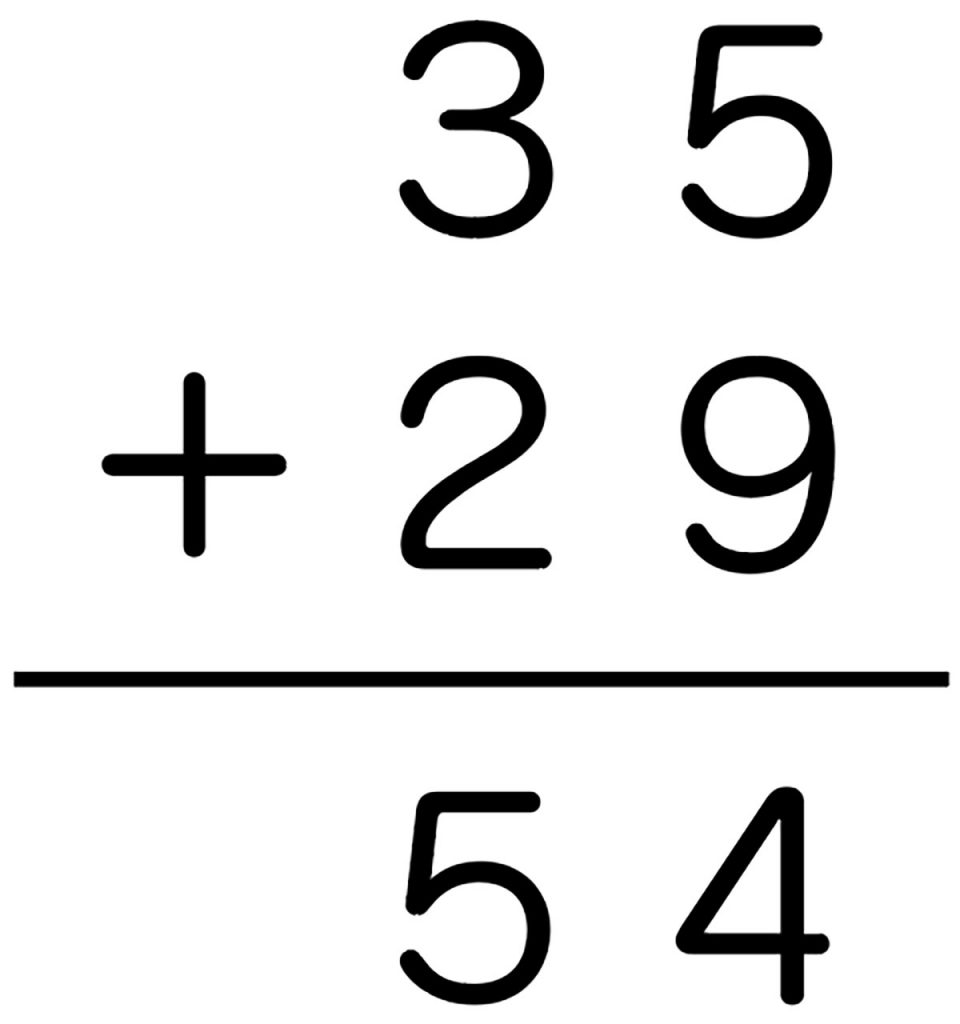
B 素朴に解いている子
筆算で書いているが、一の位と十の位の部分和を書き、非形式の筆算の形で解いている。
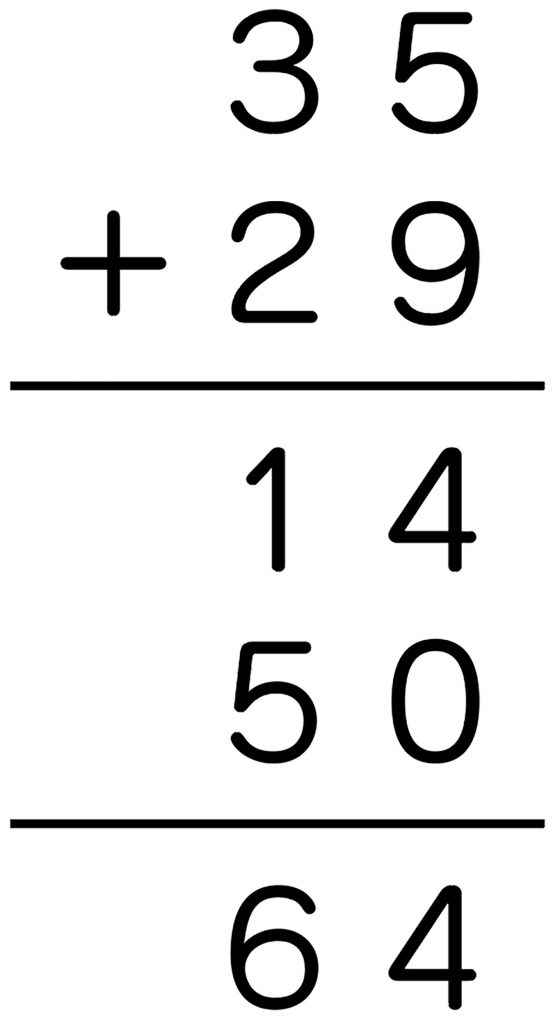
C ねらい通り解いている子
筆算形式で書き、その説明も書いている。
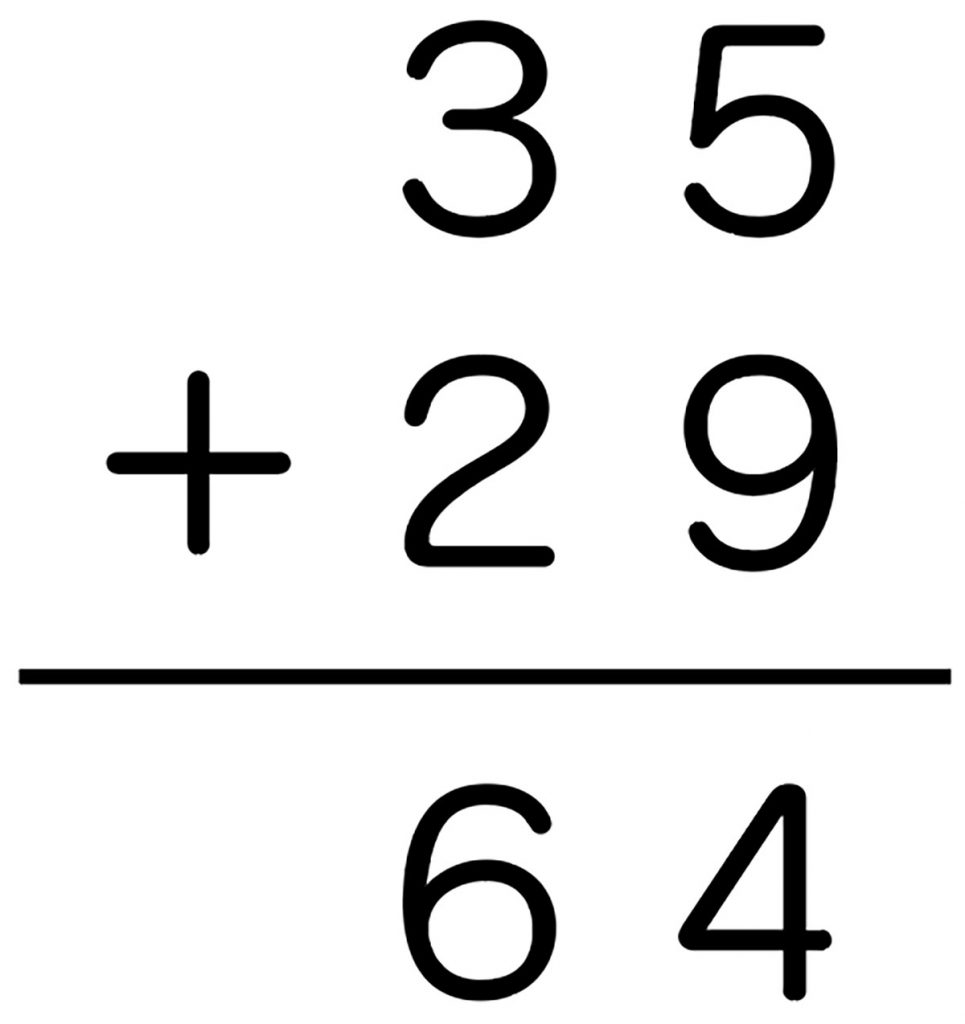
5+9=14
30+20=50
14+50=64
答えは64になる
自力解決の様子から、子供たちの状況を評価します。そして、子供たちの学習の状況によって個別指導を行ったり、一度全員の手を止めさせて、「ヒントを言える人はいるかな」と困っている子供へのヒントを出させたりするなどして、全員が解決に向けて動き出せるよう指導します。
今、答えが出せずに困っている人がいますね。その子たちにいいヒントはありませんか。
十の位は十の位、一の位は一の位で足せばいいです。
学び合いの計画
イラスト/横井智美


