小4算数「面積」指導アイデア《複合図形の面積を効率よく求めよう》
執筆/新潟県公立小学校教諭・樋浦教之
編集委員/文部科学省教科調査官・笠井健一、新潟県公立小学校校長・遠藤昇
目次
本時のねらい
本時6/11時
複合図形の面積について、長方形の数に着目することで、より効率のよい求積方法を自ら選択できる。
評価規準
凹型複合図形や凸型複合図形について、求積する長方形の数が少なくなる方法を自ら選択している。
問題
次のA・B、2つの図形の面積を求めましょう。
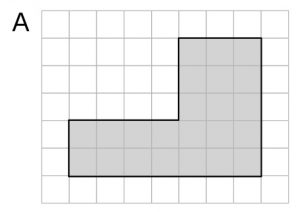
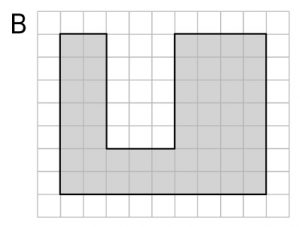
前時(第5時)に、L字型複合図形の求積方法を学習します。「分けて足す」「全体から引く」という方法があることを確認します。
第5時の最後に「別のL字型の面積を求めるとき、どちらの方法を使いますか」と、子供たちに質問します。そこで、「どちらでもいい」「どちらでも簡単に求められる」という発言を引き出しておきましょう。
Aの図形から面積を求めます。この箱の中に入っている「くじ」に書いてある方法で求めます。くじは「分けて足す」「全体から引く」の2種類です。どちらのくじが出てほしいですか。
自由に面積の方法を求めさせるのではなく、「くじ」に書いてある方法で面積を求めさせます。このことにより、Bの図形を求めるとき、「『全体から引く』というくじが出てほしい」という子供の発言を引き出します。
どっちのくじが出ても大丈夫です。
どっちが出ても簡単に面積が出せます。
(くじを引く)「分けて足す」が出ました。この方法で面積を求めましょう。
できました。縦に分けて、2つの長方形にします。
2×4+5×3=23 答えは23㎠です。
横に分けてもできます。
2×7+3×3=23
もし「全体から引く」が出ても、面積を求めることはできましたか。
できます。5×7−3×4=23 答えは23㎠です。
やっぱり、どっちのくじが出ても簡単に面積を求めることができました。
求積における「簡単」という意味を押さえておきます。ここでは「より少ない式で求められる」「効率がよい」ということを「簡単」とします。
次にBの図形の面積を求めます。どちらのくじが出ても、簡単に面積を求めることができそうですか。
どっちが出ても大丈夫です。
「全体から引く」が出たほうが「簡単」にできそうです。
えっ、どうして? 「分けて足す」でも、面積は出せそうだけど。
学習のねらい
Bの図形は、「分けて足す」より「全体から引く」ほうが、簡単に面積が求められるのか。
見通し
Bの図形を「分けて足す」もしくは、「全体から引く」なら、どのように考えて求めますか。
こうやればよいと思います。
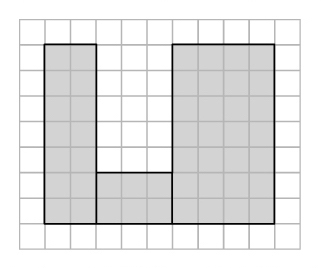
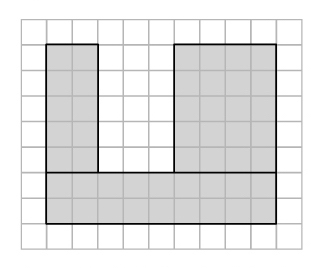
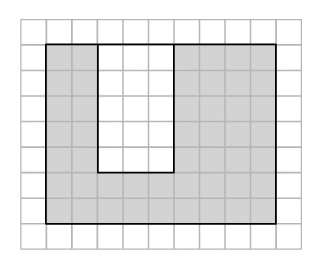
実際に「分けて足す」「全体から引く」どちらの方法でも面積を求めてみましょう。そして、どちらの方法がよいのか、自分の考えをまとめてみましょう。
自力解決の様子
A つまずいている子
Bの図形の面積を求めることができない。
B 素朴に解いている子
どちらの方法でも面積を出すことができたが、「全体から引くほう」が簡単な理由が分からない。
C ねらい通り解いている子
どちらの方法でも面積を求めることができ、式の数や長方形の数に着目して、図形Bは「全体から引く」が簡単なことに気付いている。
学び合いの計画
イラスト/横井智美
『教育技術 小三小四』2020年11月号より

