小6算数「対称な図形～点対象～」指導アイデア
執筆／埼玉県公立小学校主幹教諭・濁川 究
編集委員／文部科学省教科調査官・笠井健一、浦和大学教授・矢部一夫
目次
本時のねらいと評価規準
（本時８／12時）
点対称な図形のかき方を、点対称な図形の性質を基に考え、説明することができる。また、線対称な図形との相違点を明らかにし、点対称な図形について理解を深める。（ 思考力・判断力・表現力等）
問題場面
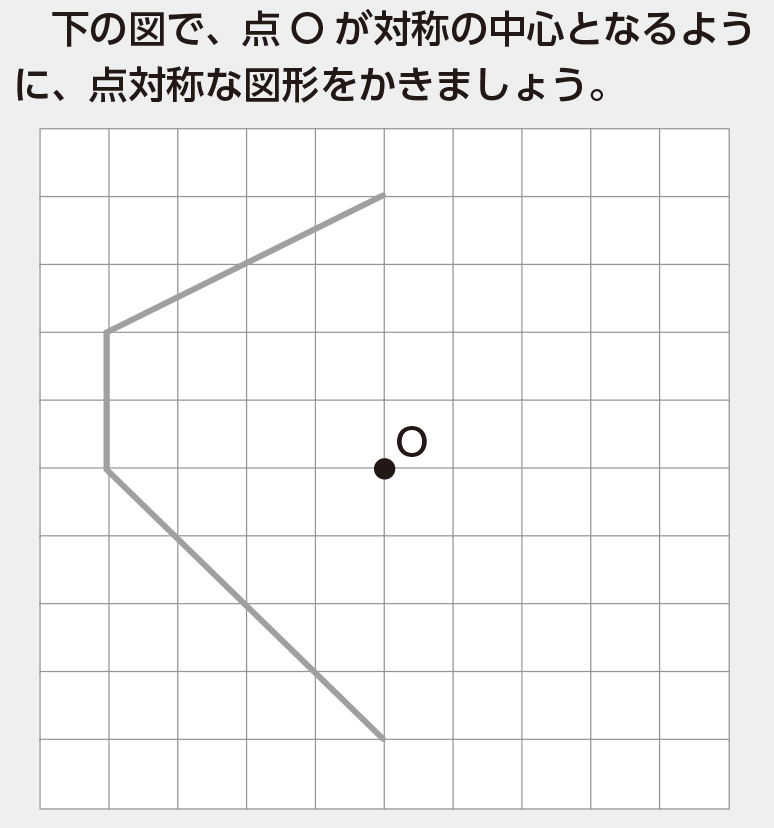
どんな形になりそうですか?
左側の形が反対向きになった形が右側にできると思います。
風車みたいな形になるかな。
線対称な図形じゃないからコマみたいな形にはならないと思います。
見通し
できあがりの形をフリーハンドでかいてみましょう。
どんなことを意識してかきましたか。
左側の図形の180°回転させた形が右側にくるようにかきました。
対称の中心と対応する点までの長さを意識しました。
右側にかく形が、左側の形の合同な形を反対にした形になっているかを意識しながらかきました。
これまで、調べてきた点対称な図形の性質が使えそうですね。
本時の学習課題
点対称な図形の性質を使って、点対称な図形のかき方を考えよう。
自力解決の様子
A つまずいている子
左側の図形の180°回転させた形が右側にくることは分かっているが、形に捉われてしまい、「対称の中心から対応する２つの点までの長さ」に着目できていない。
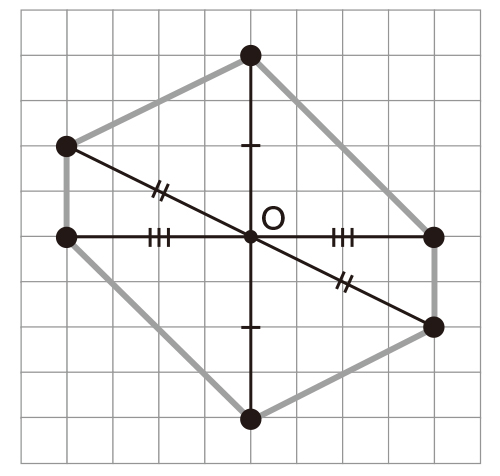
B ねらいどおり解決している子
左側の図形の頂点から対称の中心を通る直線をひき、対称の中心から頂点までの長さと、対応する点までの長さが等しくなるようにもう一方の点の位置を決めている。
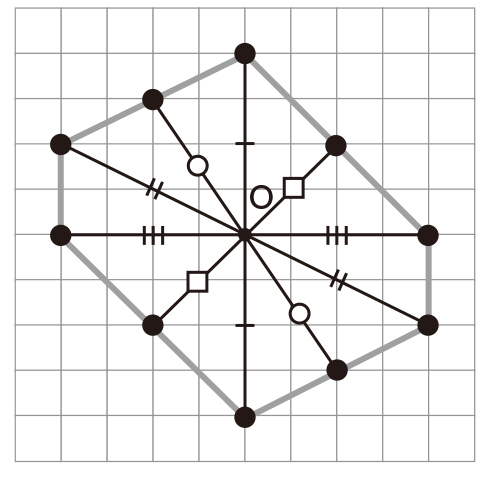
C 進んでいる子
図形上に任意の点を複数箇所とり、対称の中心を通る直線をひき、対称の中心から対応する２つの点までの長さが等しくなるようにもう一方の点の位置を決めている。
学び合いの計画
線対称な図形に比べ、点対称な図形は、対応する辺や角、点などが捉えにくくなる児童が多くなります。そこで、線対称な図形と点対称な図形との類似点や相違点について話し合うことで、点と点の位置関係で、それぞれの図形が決まることを理解できるようにします。
ノート例
全体発表とそれぞれの考えの関連付け
できあがった図形が点対称になっているか確かめましょう。
左側を写し取って、180°回転させるとぴったりと重なるので点対称な図形になっています。
対応する辺の長さや角の大きさがすべて等しくなっています。
対称の中心から対応する２つの点までの長さはどこも等しくなっているので、点対称な図形がかけていると思います。
Bの点対称な図形は、どんなかき方をしていますか。
もともとの形の頂点から、対象の中心を通る直線をひいています。
ひいた直線のどこかに対応する点があるので、対称の中心から２つの点までの長さがそれぞれ等しくなるところを見つけています。
なぜ、このようにかくと対称な図形がかけるのでしょうか。
対称な図形は対応する２つの点を結ぶ直線は、必ず対称の中心を通るという性質があるからです。
対称な図形は、対称の中心から対応する２つの点までの長さは、等しくなっているからです。
Cも同じように対称な図形がかけていましたが、B と同じところや違うところはありますか。
Cも対称な図形の性質を使ってかいているところがBと同じです。
Bと違うところは、頂点以外の点も対称の中心を使っているところです。
Cのかき方からどんなことが言えますか。
対称な図形は、対称の中心から対応する２つの点までの長さが同じだったら、頂点だけでなく、もとの図形のどの点をとってもかけます。
もとの図形の線対称な図形をかくとこのようになります。かき方で似ているところや違うところはありますか。
どちらも、対応する２つの点を見つけているところは似ています。
対応する２つの点の見つけ方が違います。
線対称な図形は、２つの点を結ぶ直線が垂直に交わっていて、点対称な図形は対称の中心を必ず通るところが違います。
対称の軸と直線が垂直に交わる点から、２つの対応する点までの長さを等しくかいているところと、対称の中心から２つの対応する点までの長さを等しくかいているところが似ています。
まとめ
- 点対称な図形は、頂点や図形上の点から対称の中心を通る直線をひき、対称の中心と対応する２つの点の長さが等しくなるように点を決めるとかくことができる。
- 対応する点をつなげた直線どうしが対称の中心で交われば、点対称な図形である。
評価問題
点Oが対称の中心になるように、点対称な図形をかきましょう（方眼なし）。
子供に期待する解答の具体例
対応する２つの点を結ぶ直線が対称の中心を通ることと、対称の中心から対応する２つの点までの長さが等しいことを使ってかいた。
※等しい長さを写しとる道具としてのコンパスの有用性についても触れる。
感想例
- 点対称な図形をかくときは、対称の中心をもとに対応する点を見つければよいことがわかりました。
- 点対称な図形の性質を使うと、点対称な図形がかけました。
イラスト／オモチャ、横井智美
『教育技術 小五小六』 2021年4/5月号より
