小3算数「九九表とかけ算のきまり」指導アイデア（9/9時）《九九の範囲を超えるかけ算を考える》
執筆／富山県公立小学校教諭・前田正秀
編集委員／文部科学省教科調査官・笠井健一、前・富山県公立小学校校長・中川愼一
目次
本時のねらいと評価規準
（本時９／９時 単元終末の発展的な学習）
本時のねらい
九九の範囲を超えるかけ算を、九九や十の段のかけ算を活用して考える。
評価規準
かけられる数が10 を超える場合の答えの求め方を、図や式を用いて表し、九九や十の段のかけ算を活用して考えている。（思考･判断･表現）
問題
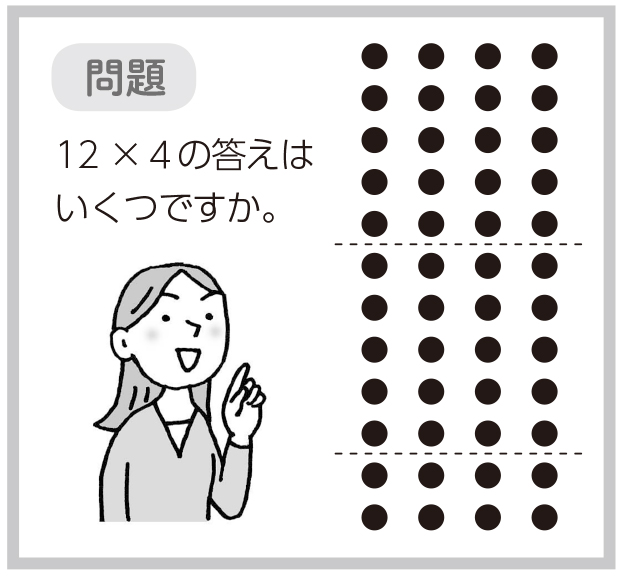
（６×４に並んだチョコの写真を提示）チョコは、何個ですか。
６×４で24個です。
（10×４に並んだチョコの写真を提示）チョコは、何個ですか。
10 ×４で40個です。
では、これは何個でしょう。（12×４に並んだチョコの写真を提示）
式は12×４だけど…。
九九の範囲を超えているよ。
でも、求められそうだよ。だって、６×４の２倍だから…。
それに、10×４より２×４だけ多いから…。
それでは今日は、12×4 を使って九九を超えるかけ算の答えの求め方を考えていきましょう。
学習のねらい
九九をこえるかけ算の答の求め方を考えよう。
見通し
九九を超えるかけ算も、九九や十の段のかけ算をうまく使えば、答えを求めることができる。〔方法の見通し〕
自力解決の様子
A つまずいている子
12＋12＋12＋12＝48
・たし算に戻して考えようとしている。
B 素朴に解いている子
６×４＝ 24
24＋24＝48
・12 を６と６に分けて考えている。
「12の段＝６の段＋６の段」
C ねらい通り解いている子
10×４＝40 ２×４＝８
40＋8＝48
・12を10と２に分けて考えている。
「12の段＝10の段＋２の段」
学び合いの計画
学び合いは、互いの考えを理解することから始まります。考えを発表させる際には、一人の子供にすべてを語らせるのではなく、友達の描いた図から、どんな式になるかを想像させたり、友達の書いた式を言葉で説明させたりするとよいでしょう。図と式と言葉を結び付けることで、互いの考えを理解しやすくなります。
イラスト／小沢ヨマ、横井智美
『教育技術 小三小四』2021年4/5月号より
