小4算数「分数をくわしく調べよう」指導アイデア
執筆/埼玉県公立小学校教諭・杜多奈月
編集委員/文部科学省教科調査官・笠井健一、浦和大学教授・矢部一夫
目次
本時のねらいと評価規準
本時6/9時
ねらい
同分母の分数の加法計算の意味を理解し、その計算ができる。

評価規準
同分母の分数の加法計算の意味を理解している。(知識技能)
どのような式になると思いますか。
2枚を合わせるので、 [MATH]\(\frac{4}{5}\)[/MATH]+ [MATH]\(\frac{3}{5}\)[/MATH] のたし算になると思います。
分数と分数をたせるのかな。
分数のたし算のようですね。分数もたし算ができるのでしょうか。
整数では3+5、小数では0.5+0.3とできたので、分数でもできると思います。
今まで、整数+整数、小数+小数を勉強してきました。分数も「数」の仲間なので、たし算ができそうですね。
では、分数+分数をどうやって計算すればよいか、計算のしかたを考えましょう。
学習のねらい
分数+分数の計算のしかたを考えよう。
見通し
小数の0.5+0.3のときは、0.1を基にして考えたので、今回も基にする数を決めて、その数のいくつ分と考えればよいと思います。
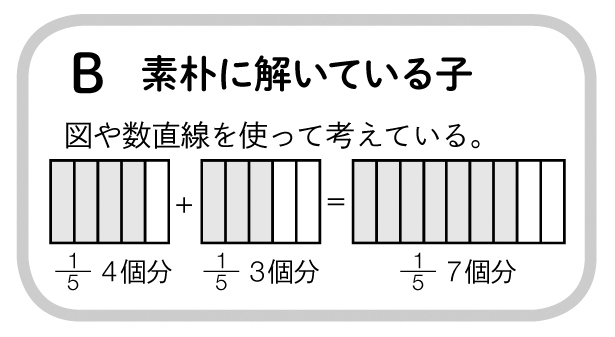
図や数直線に表して考えればよいと思います。
【誤】分母どうし、分子どうしをたして計算するのかな?
自力解決


学び合いの計画
イラスト/小沢ヨマ
『教育技術 小三小四』2020年2月号より