「五角形の角の和を求め、その方法を説明しなさい」【｢高校につながる英・数・国｣の授業づくり #49】

2025.10.10

「540度はどうやって求めた？」と問うと、「教えられました」という子供が大半

まず紹介していただく授業は、２年生の「平行と合同」の単元の中の「多角形の内角の和」について考える授業です。学習指導要領解説に示された「算数・数学の学習過程のイメージ」図の「数学の事象」に関わる、「多角形の内角の和」の授業の展開について、鷹野教諭は次のように説明します（資料１参照）。

資料１　「多角形の内角の和」の指導案

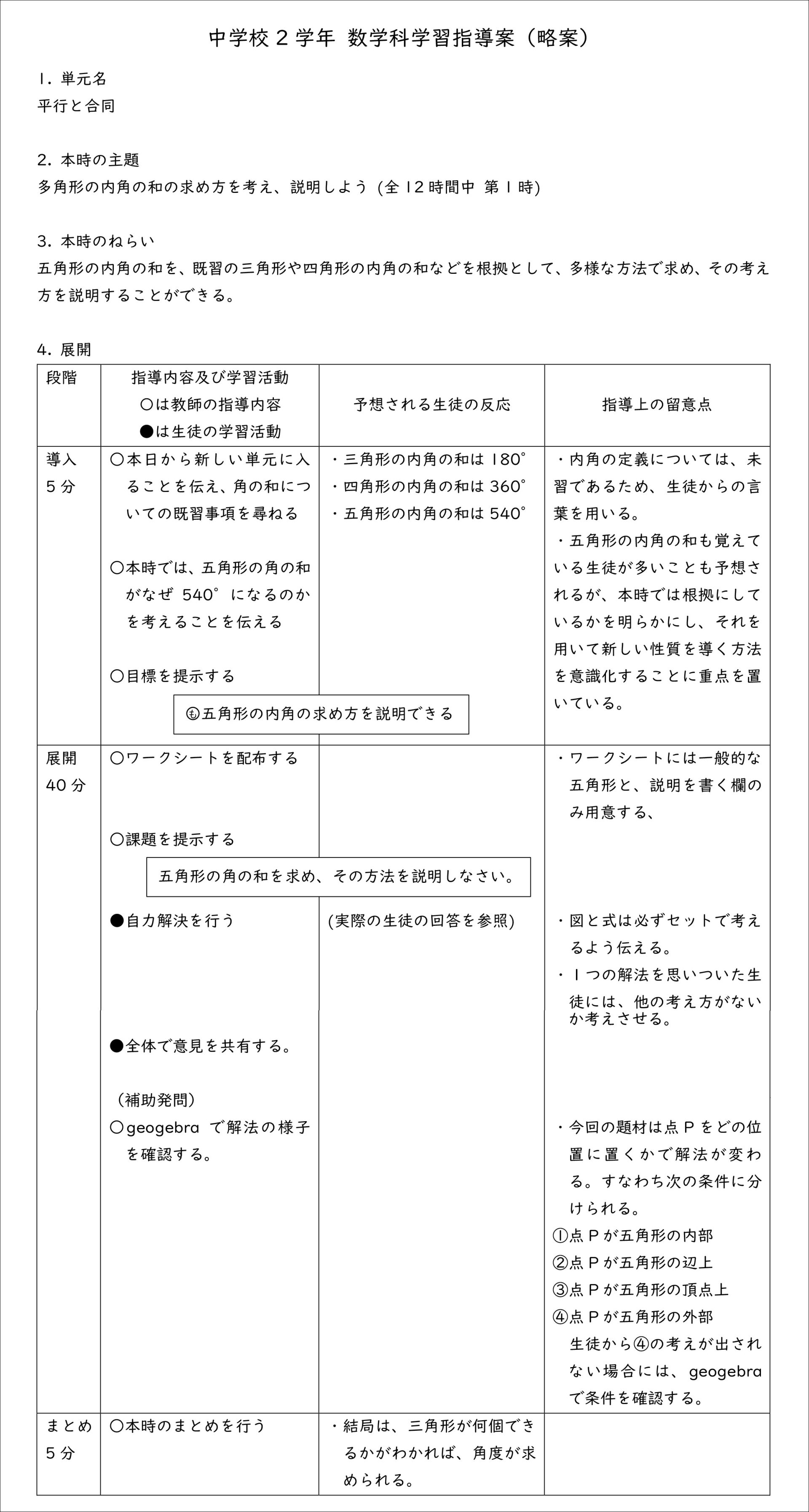
「授業の最初に、『今から図形の単元を学習するんだけど、三角形の内角の和は何度だっけ？』と既習について尋ねると、『180度です』とすぐ返ってきます。四角形も『360度』と答えますが、『じゃあ五角形は？』と問うと、クラスの３分の１くらいが『540度です』と答えられるというような状況です。

次に『この540度って何でそうなるの？　どうやって求めた？』と問うと、『教えられました』という子供が大半です。そこで『じゃあ、どうしてそうなるのか、一緒に考えていこうよ』というところから、目標の『五角形の内角の求め方を説明できる』を提示して学習に入っていきます。

これは余談ですが、本県では、東京書籍の教科書を使っています。この教科書のおもしろいところは、三角形の内角の和180度を使って五角形の内角の和を求めるのですが、そこに立ち返って、『そもそも三角形の内角の和はなぜ180度なのか？』と考えていくところです。最終的にはそこにつながっていくのがおもしろいところだと思います」

GeoGebraを使って、子供たちに自由に操作をさせる

授業では目標を設定したら、複数の五角形と説明記入欄のみ記されたワークシートを配付し、「五角形の角の和を求め、その方法を説明しなさい」と課題を提示し、まずは自力解決に取り組んでいくという鷹野教諭。机間を回りながら、声をかけたり教室全体に投げかけたりしていくと話します。

「自力解決を図っていくと、子供の大半は頂点上から補助線を２本引いて、３つの三角形に分けます。また、（四角形の内角は三角形を根拠にしているため）論理的な説明としては不十分な三角形と四角形に分けるという子供もいます。それも、『三角形と四角形に分けるのもおもしろいね』と評価します。

ただ、五角形の内部に点を設定して三角形に分割する子供はごく一部の数学が得意な子供のみで、辺上や外部に設定する子供はいません。そこで、机間巡視しながら、『（補助線を引く点が）頂点上だけだと気持ち悪くない？』『他に方法はないかな？』と全体に投げかけるのです。

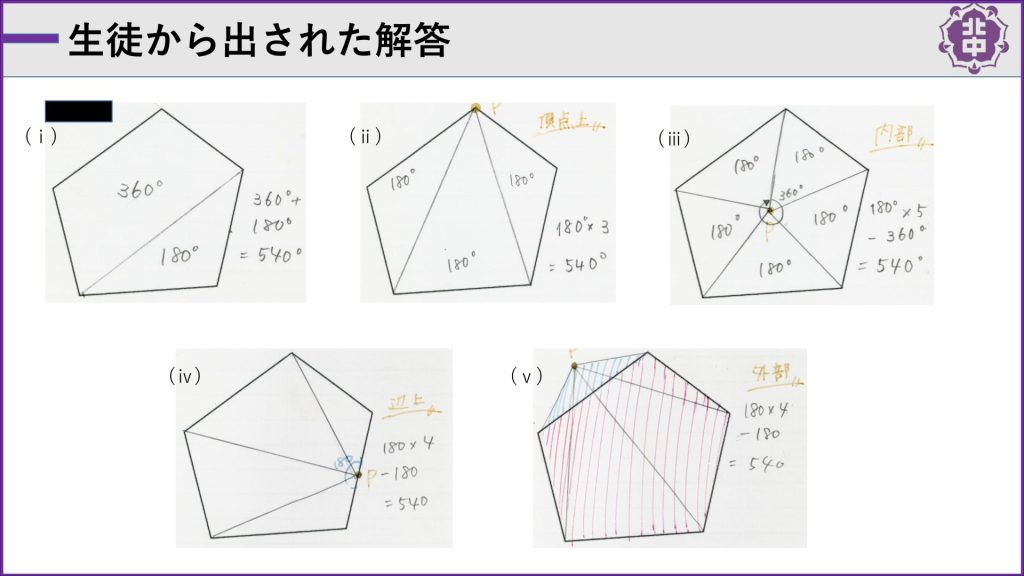
すると『辺上でもできるかも』など、多様な考えが出てきます。そこで、GeoGebra（数学ソフト）を使って、子供たちに自由に三角形に分割するための頂点を操作させると、『辺上でもできそうだぞ』『内部でもできそう』『外部でもできるよ』と多様な解決方法が出てきます。そうして、多様な解決の可能性が見えてきたら、また個人で探究させていくのです（資料２参照）」

そうやって、多様な解決方法が出されていき、それを全体で共有した後で、授業の最後に、「三角形が何個できるかが分かれば、多角形の内角の和は求められる」というまとめを子供たちから出してもらって授業を終えたそうです（資料３参照）。

資料２　子供たちの解法のバリエーション