小６算数「角柱と円柱の体積」指導アイデア《図形の構成要素に着目し、三角柱の体積の求め方を考える》
執筆／富山県高岡市立木津小学校教諭・屋鋪善祐
監修／東京都国立教育政策研究所教育課程調査官・加固希支男、富山大学附属小学校教諭・羽柴直子
目次
年間指導計画
・対照な図形
・文字を使った式
・場合の数
・分数×÷整数
・円の面積
・分数×分数
・分数÷分数
・角柱と円柱の体積
・資料の調べ方
・小数と分数の計算
・比と比の利用
・拡大図・縮図
・比例と反比例
・およその面積と体積
・算数のまとめ
単元の展開（各時の主な学習活動内容）
第１時 第５学年で学習した体積の学習をふり返り、体積の意味を確認する。
第２時 図形の構成要素に着目し、直方体の体積を求める公式を捉え直し、四角柱の体積の求め方を考える。
第３時（本時）図形の構成要素に着目し、三角柱の体積の求め方を考える。
第４時 図形の構成要素に着目し、円柱の体積の求め方を考える。
第５時 図形の特徴に着目し、直方体を組み合わせた複合図形を角柱と見て、体積の求め方を考える。
第６時 学習内容の習熟・定着を図る。
本時のねらい
図形の構成要素に着目し、三角柱の体積の求め方を考える。
評価規準
角柱の体積の求め方について、図形の構成要素に着目して、既習の角柱の求め方を基にしたり、図形の面積の学習と関連付けたりして考えている。
本時の教材のポイント
角柱の体積の求め方を考える授業では、体積を求める公式を単に覚えるのではなく、どうしてこのように求めることができるのか、公式を見いだす過程が大切です。そこで、三角柱の体積を求めるために、前時に学習した四角柱の体積の求め方や、第５学年「三角形の面積」で学習したことを想起し、体積の求め方を考えていきましょう。
今回、扱う題材は下図のような形・数値の三角柱です。問題提示の際は、これまで学習した図形と比較し、共通点や違いを出し合ったり、「どのように求めればいいかな？」など全体に投げかけたりすることで、解決の見通しをもち、自分の考えをもつことができるようにします。また、図形が描かれたワークシートを用意することで、自分の考えを自信をもって表現することができるようにしたり、デジタルコンテンツで図形を変形させ、互いの考えを可視化したりすることも有効です。
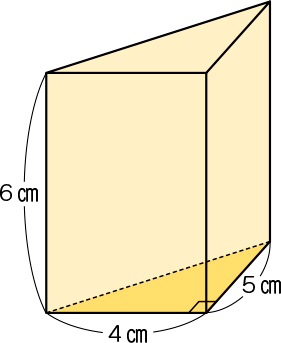
また、三角柱の体積を求める際、三角柱と四角柱の関係を捉えられなかったり、三角形の面積を求める段階でつまずいたりする子供が出てくることが想定されます。そこで、同じ三角柱を２つ合わせると四角柱になることに気付くことができるように、実際の立体模型を用意し、操作しながら考えることができるようにしたり、既習の三角形の面積の公式を想起する場を設けたりすることが大切です。友達がどこでつまずいているのか一緒に考え、学びを深める場の設定も有効です。
本時の展開
前回の授業では、この形の体積を求めましたね。何という形でしたか。
四角柱です。
どのように求めましたか。
「底面積×高さ」で求めました。
そうでしたね。では、今日はこの図形です。
下の三角柱の体積は、何㎤ですか。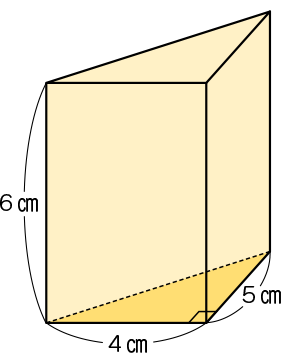
あ、三角柱です。
さあ、どのように求めればいいのでしょう。
四角柱を半分にしたら三角柱だから、四角柱の求め方を使えばいいと思います。
四角柱の求め方のように、高さ１cmの三角柱の体積に注目すればいいと思います。
それでは、自分なりの方法でやってみましょう。
三角柱の体積の求め方を考えよう。
見通し
四角柱を半分にした形として求めてみよう。
高さ１cmの三角柱の体積を基に、「底面積×高さ」として求めてみよう。
自力解決の様子
Ａ つまずいている子
・三角形は四角形を半分にした形だと捉えられない。三角形の面積の求め方が分からないでつまずいている。
Ｂ 素朴に解いている子
・５年「三角形の面積」の学習を想起し、三角形は四角形を半分にした経験から、四角柱を半分にして三角柱の体積を求めようと考えている。
Ｃ ねらい通り解いている子
・四角柱の体積の求め方と同じように、高さ１cmの三角柱の体積を表す数と、底面積を表す数は等しくなることに気付き、関連付けながら考えている。
ノート例
全体発表とそれぞれの考えの関連付け
どのように求めましたか。
（Ａさん） 私は、この三角柱を四角柱の半分と見て求めました。四角柱は、４×５×６＝120。120㎤なので、半分にすると120÷２＝60。60㎤になりました。
（Ｂさん） Ａさんと同じ考えです。図に表すと、このようになりました。
ちょっと待ってください。三角柱が四角柱の半分とは、どういうことですか。
僕もよく分かりませんでした。
（Ｂさん） 図に表すと、このようになります。三角柱を２つ合わせると四角柱になります。
う～ん、分かるような分からないような……。
実際に三角柱を用意しました。これを使って考えてみましょう。
※各自操作する。
あっ！ 分かりました。確かに、同じ三角柱を２つ合わせると四角柱になります。
四角柱の半分が三角柱というのは、こういうことだったのですね。
これなら、昨日みんなで学習した四角柱の体積を求める考え方を使って、三角柱の体積も求められます。
（Ａさん） 「三角柱が２つで四角柱」で思い出したのですが、５年生の面積の学習ともつながります。三角形が２つで四角形になりました。
体積の学習と面積の学習がつながったような気がします。
（Ｃさん） 私は、違う考え方をしました。前回の授業で、四角柱の体積を求めるとき、高さ１cmの四角柱の体積を表す数と、底面積を表す数が等しくなると分かりました。なので、今回の三角柱の場合も、高さ１cmの三角柱の体積を表す数と、底面積を表す数が等しくなると考えました。
（Ｄさん） 僕も同じように考えました。でも、答えが60㎤にならなくて困っています。
Ｄさんは、考え方は一緒だけれど、困っているんですね。どんな式を立てたのですか。
（Ｄさん） ４×５×６＝120。120㎤です。
みなさん、Ｄさんの式をどうすればいいと思いますか。
（Ｅさん） Ｄさんがどこで困っているか分かりました。三角形の面積の公式は「底辺×高さ÷２」なのに、÷２をしていません。なので、Ｃさんの考えに合う式は、「４×５÷２×６＝60」だと思います。
Ｄさん、Ｅさんの考えを聞いてどう思いましたか。
（Ｄさん） 確かに！ 自分が三角形の面積の求め方を勘違いしていたことに気付きました。
求めることができて、よかったですね。さあ、２つの考え方が出てきましたね。２つの式を見比べてみましょう。
どちらの式でも答えは一緒です。
数を並べ替えると、同じ式「４×５÷２×６＝60」になります。
これは、「底面積×高さ」の式です。
四角柱のときと一緒ですね。
つまり、三角柱や四角柱など、角柱の体積を求める公式は、どんな式になると言えますか。
「底面積×高さ」です。四角柱と三角柱では、全然違う形に見えるけれど、公式は同じになることが分かりました。
全然違う形だから、全然違う公式になると思っていたけれど、みんなで学習をしたことで、なぜ同じになるのかよく分かりました。
まとめ
- 三角柱の体積は、「底面積×高さ」で求めることができる。
- 三角柱や四角柱などの角柱の体積は、「底面積×高さ」で求めることができる。
では、評価問題で、様々な角柱の体積を求めてみましょう。
評価問題
下の角柱の体積を求めましょう。
子供に期待する解答の具体例
①底面は三角形。
６×４÷２×５＝60
60㎤
②底面は台形。
（５＋７）×８÷２×６＝288
288㎤
感想例
- ・三角柱の体積は、「底面積×高さ」で求めることができることが分かりました。
- ・前回と今回の授業で、三角柱と四角柱の体積は、「底面積×高さ」で求められることが分かりました。これからは、他の角柱でも求めることができるのか、試してみたいです。
ポイント＆アドバイス
構成／桧貝卓哉 イラスト／横井智美 図版作成／永井俊彦