小４算数「小数のしくみ」指導アイデア《面積図を用いて小数の相対的な大きさを考える》

特集: 文部科学省教科調査官監修｢教科指導のヒントとアイデア｣

2024.10.23

単元の展開

第１・２時　　十進構造の単位の構成に着目し、[MATH]\(\frac{1}{1000}\)[/MATH]の位までの小数の表し方を考察
▼
第３時　　　　整数の仕組みに着目し、小数の構成や位取りの原理を類推し考察
▼
第４時　　　　十進位取り記数法の原理に着目し、小数の大小関係を考察
▼
第５時　　　　位の変わり方に着目し、小数を10倍した数や[MATH]\(\frac{1}{10}\)[/MATH]した数を考察
▼
第６時（本時）十進位取り記数法の原理に着目し、小数の相対的な大きさの表し方を考察
▼
第７時　　　　十進位取り記数法の原理に着目し、[MATH]\(\frac{1}{100}\)[/MATH]の位、[MATH]\(\frac{1}{1000}\)[/MATH]の位の小数の加法の筆算の仕方を考察
▼
第８時　　　　十進位取り記数法の原理に着目し、[MATH]\(\frac{1}{100}\)[/MATH]の位、[MATH]\(\frac{1}{1000}\)[/MATH]の位の小数の加法（小数の桁数が揃っていない場合）の筆算の仕方を考察
▼
第９時　　　　十進位取り記数法の原理に着目し、[MATH]\(\frac{1}{100}\)[/MATH]の位、[MATH]\(\frac{1}{1000}\)[/MATH]の位の小数の減法の筆算の仕方を考察
▼
第10時　　　　十進位取り記数法の原理に着目し、[MATH]\(\frac{1}{100}\)[/MATH]の位、[MATH]\(\frac{1}{1000}\)[/MATH]の位の小数の減法（小数の桁数が揃っていない場合）の筆算の仕方を考察
▼
第11時　　　　数の合成・分解や相対的な大きさの表し方に着目し、小数を多様な見方で表す方法の考察
▼
第12時　　　　学習内容の生活への活用
▼
第13時　　　　学習内容の習熟や定着、数学的な見方・考え方のふり返り

本時のねらい

面積図を用いて、0.01の大きさに着目して、小数の相対的な大きさについて考え、説明することができる。

評価規準

・[MATH]\(\frac{1}{100}\)[/MATH]の位の単位に着目して、図や位取り表を使って小数の相対的な大きさについて考え、説明している。
・小数について、0.01の単位を用いて相対的な大きさを捉えることができる。

本時の展開

これ（図１）を１とするとき、0.1はどのように表すことができますか｡（少し時間をとって）指でイメージを空中に書いてみてください。

※子供たちが空中で0.1の図を描く。

では、前に出て来て、黒板に書いてみてください。

※子供が黒板に書く。

そうですね｡（図２を示しながら）このような形になりますね。これは、１の形に対してどのような形になっていますか。

１を10等分した１つ分が0.1だから、10等分した形になっています。

そうですね。では、さらに0.1を基にすると、0.01はどのように表すことができますか。同じように前に出て来て書いてください。

※子供が黒板に書く。

とても小さい形ですね｡（図３を示しながら）このような形になりますね。これは、0.1の形に対してどのような形になっていますか。

0.1を10等分した１つ分が0.01だから、10等分した形になっています。

そうですね。

他にも、１を100等分した１つ分とも言えます。

たしかにそうですね。図１と図３を比べたとき、１を100等分したら0.01になることがイメージできますか。

（ジェスチャーで示しながら）こんなふうに、縦も横も10等分したら、10×10で100等分になって0.01の形ができます。

そうですね｡（下のように板書しながら）ちなみに、逆から見ると、0.01を何個集めたら0.1になりますか。

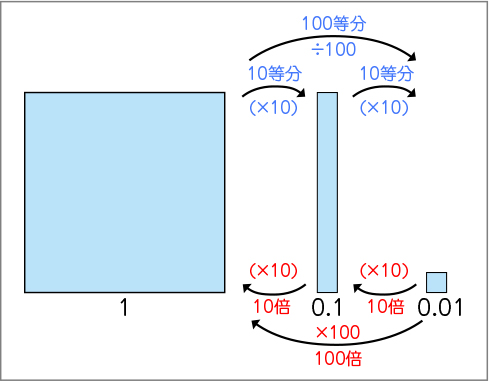
10個です。

では、0.1を何個集めたら１になりますか。

10個です。

では、0.01を何個集めたら１になりますか。

100個です。

（下の図を提示して）では、ちょっとこれを見てください。これはいくつを表していますか。

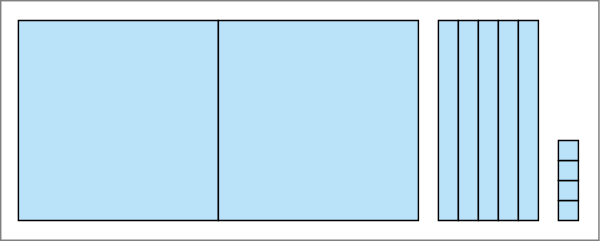
2.54です。

どうしてですか。

だって、１が２個で、0.1が５個で、0.01が４個あるからです。

そうですね。今日はこの2.54という数について考えていきたいと思います。2.54は、（図３を示しながら）この0.01を何個集めた数ですか。

2.54は0.01を何こ集めた数ですか。0.01をもとにして小数の大きさをとらえましょう。

見通し

（下のように、0.04を表す図に、0.01を表す図３を当てながら）2.54の0.04は0.01を何個集めた数ですか。

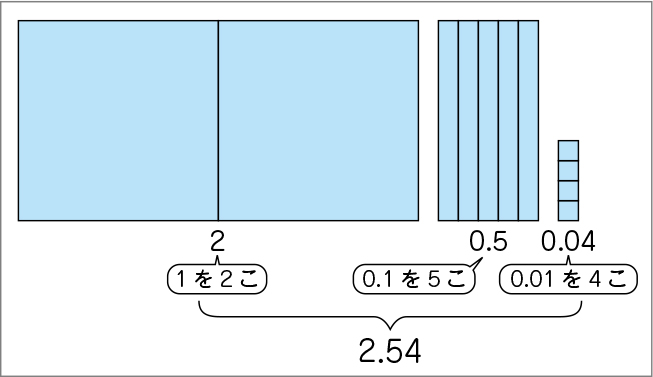
４個です。

そうですね｡（0.01を表す図３を当てていきながら）１、２、３、４で0.04は0.01を４個集めた数ですね。このように、0.5や２についても0.01をいくつ集めた数かを考えて、2.54は0.01をいくつ集めた数なのかを説明しましょう。　

※ワークシートと、基となる0.01を表す１辺１cmの方眼（包含用紙をカットしたもの）を配付する。

ワークシート（ダウンロード可）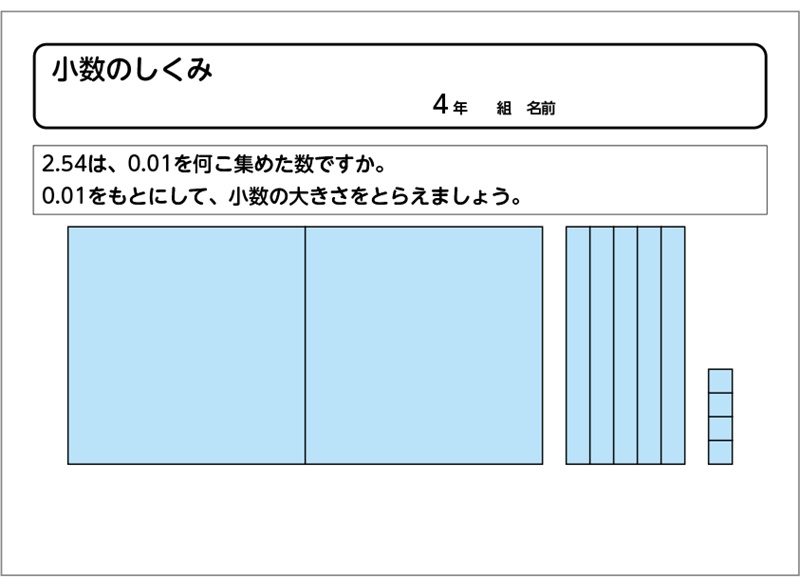

ダウンロードはこちら＞＞

自力解決の様子

Ａ　つまずいている子
・どのように考えていったらよいのか悩んでいる。
・考えを書くことができない。

Ｂ　素朴に解いている子
・254個
・小数点を取って254個

Ｃ　ねらい通り解いている子
・２ …0.01が200個
・0.5 …0.01が 50個
・0.04…0.01が４個
・200＋50＋４=254　254個

学び合いの計画

何を問われているのか分からずに困っている子や、配られたワークシートと１辺１㎝の方眼紙を基にどのように考えたらよいのか分からずに悩んでいる子もいます。考えている際中であれば、その姿勢を価値付けて励ますようにしましょう。

また、困っているようであれば、１辺１㎝の方眼紙を0.1を表す図に当て、｢Ｔ：0.1を表すこの棒に0.01は何個入りますか？」｢Ｃ：10個です」｢Ｔ：そうですね、10個ですね。10個が分かるように、線を入れてごらん」｢Ｃ:（線を入れる）」｢Ｔ：いいですね。では、５つ分、0.5には0.01は何個入りますか」｢Ｃ：50個です」｢Ｔ：そうですね。0.5は0.01を50個集めた数になりますね」と、実際に操作をし、線を書き入れながら、やりとりを通して一緒に考えていきます。そして、｢では、同じように考えて、２は0.01を何個集めた数だろう？」と問いかけ、子供が考え方を理解し、説明できるようにしていきます。

単に “254個” とだけ書いている子や “小数点を取って254個” と書いている子もいます。このような場合には、｢どうして254個になるのですか」｢小数点を取るだけでどうして答えが出せるのですか」と問いかけ、上記Ｃのような考えを口頭で説明することができた場合には、｢なるほど、それも書いておこう」といった声かけをしていきます。

自力解決後は、グループのなかで考えを説明し合う時間をとるようにします。このようにグループのなかでも、考えを聞き合う場をつくり、自分の考えを相手に伝える力も育んでいくようにしましょう。

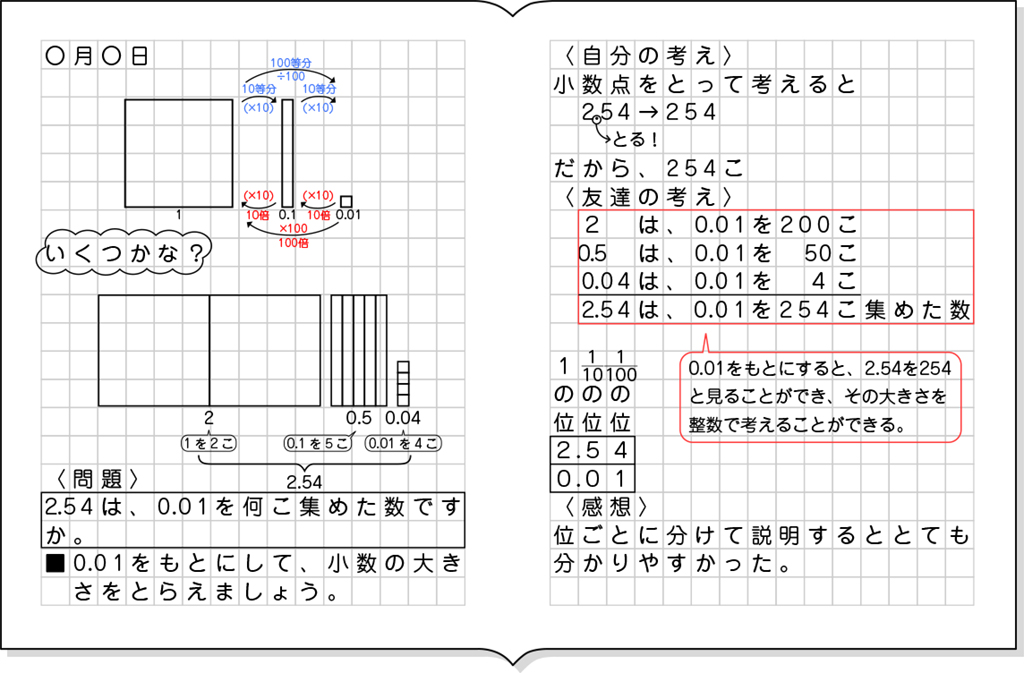
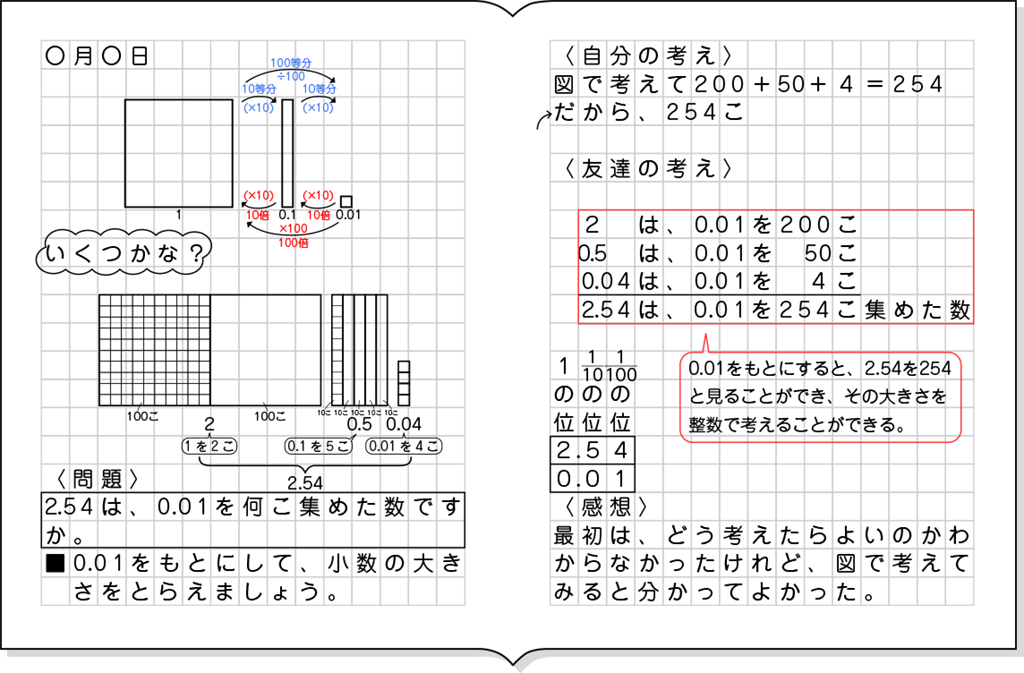
ノート例

Ｂ　素朴に解いている子

Ａ　つまずいている子　

全体発表とそれぞれの考えの関連付け

自分で考えた後、グループでも説明し合ってもらいました。2.54は0.01を何個集めた数ですか。

254個です。

どのように考えましたか。

２と0.5と0.04に分けて考えて、最初に確認したように、0.04は0.01が4個分で、0.5は0.01が50個分で、２は0.01が200個分だから、合わせて2.54は0.01が254個分になります。

※子供の言葉を基に、例えば下のように板書して考えをまとめていく。なお、子供の説明が0.04は……、0.5は……、２は……の順の場合は、「２から書かせてもらいますね」と言いながら、大きい位の数から書いていく。

では、今言ってくれたことを、図を基にみんなで確認していきましょう。0.1を表す図２の中に、0.01を表す図３はいくつ入りますか。

10個です。

そうすると、0.5を表す図４の中には、0.01は何個ありますか。

50個です。

そうですね。誰か、それが分かるように線を入れてください。

※線を入れる。

（0.01を表す図３を重ねながら）0.1は0.01が10個、0.5はその５個分で0.01が50個集まった数ですね。同じように、１を表す図１の中に、0.01を表す図３はいくつ入りますか。

100個です。

そうすると、２を表す図５の中には、0.01は何個ありますか。

200個です。

そうですね。誰か２人で協力して、それが分かるように線を入れてください。

※線を入れる。時間的余裕がない場合には、教師のほうで示す。

（0.01を表す図３を重ねながら）１は0.01が100個、２はその２個分で、0.01が200個集まった数ですね。

学習のまとめ

※上記のやりとりを通して、下のように、まとめていく。

0.01を基にすると、2.54は254と見ることができ、その大きさを整数で考えることができる。

評価問題

【１】次の①～④の数は、0.01を何こあつめた数ですか。
　①0.07　　②0.28　　③5.06　　④3.6

【２】（　　）にあてはまる数を〔　　〕の中から選んで書きましょう。
　　〔　0.01　　0.1　　1　〕
　①3.62は、（　　　）を362こ集めた数です。
　②36.2は、（　　　）を362こ集めた数です。
　③362は、（　　　）を362こ集めた数です。

解答例

【１】
①７個　②28個　③506個　④360個
【２】
①0.01　②0.1　③１

感想例

2.54は0.01を基にすると、254と見ることができ、整数で表すことができると分かった。
位ごとに分けて説明すると、とても分かりやすかった。
2.54は0.01を何個集めた数かを考えました。最初はどう考えたらよいか分からなかったけど、図で考えてみるとイメージができて、分かりやすかった。

１人１台端末活用アイデア

端末を活用し、端末上に示された前出のワークシートに自由に直線を書き込んだり、0.01や0.1を表す形を、コピー＆ペーストして重ねたりできるようにしましょう。書き込まれたものを互いに見合い、説明し合うことで、見方・考え方を広げ深めることができます。また、考えるきっかけをつかめていない子には、友達の取り組みを見ることを通して、そのきっかけをつかめるようにするなどの方法も考えられます。