小5算数「円と正多角形」指導アイデア《円の直径の長さと円周の長さの関係》

執筆/富山県射水市立大島小学校教諭・前田正秀
監修/文部科学省教科調査官・笠井健一
前・富山県南砺市立福光東部小学校校長・中川愼一

目次
単元の展開
第1時 辺や角に着目し、正多角形の定義や性質を理解する。
▼
第2時 正多角形の性質に基づき、円の中心の周りの角を等分して正多角形をかく方法を考える。
▼
第3時 正多角形や円の定義や性質に基づき、円を使って正六角形をかくことができる理由を考え、説明する。
▼
第4時 正多角形の性質に基づき、円周と直径の関係について考える。
▼
第5時(本時)円の直径の長さと円周の長さの関係について考える。
▼
第6時 円周率について知り、円周の長さや直径の長さを求める問題を解決する。
▼
第7時 円周の長さと直径の長さの関係を、比例という観点から捉える。
▼
第8時 本単元の学習内容の定着及び円周の長さを活用する問題を解決する。
本時のねらい
円の直径の長さと円周の長さの関係について考える。
評価規準
円を構成する要素である直径と円周の関係に着目し、比例の関係にあることについて筋道を立てて考えている。(思考・判断・表現)
本時の展開

円を1回転させると、どこまで進むでしょう。
円盤を転がして考える
厚紙や段ボールで作った円形の盤を転がして、一回転で進む長さを予想します。
最初は、当てずっぽうで予想するしかありませんが、さまざまな大きさの円を転がすうちに、子供たちから「さっきの円より大きいから、ここくらいかな」などの声が聞こえ始めることでしょう。予想に根拠が生まれてくるのです。
子供たちは、生活経験から、円の大きさが大きいほど円周が長くなることは知っています。子供たちのつぶやきを取り上げながら、そうした生活経験を、「直径と円周は比例する」という算数の知識へと導いていきます。
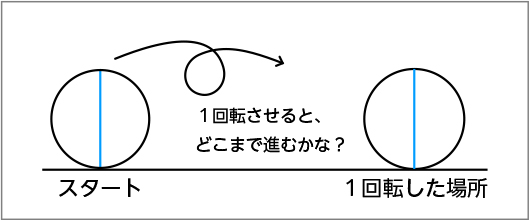
大きさの異なる円盤を転がして考える
次は、この円を転がします。1回転でどこまで進むと思いますか。
(予想する場所を指さしながら)ここまで進むと思います。さっきの円より大きいから、さっきより進むと思いました。
大きい円のほうが、遠くまで進むと思うのですね。
僕は、もっと進むと思います。(予想する場所を指さしながら)ここまで進むと思います。さっきの円の2倍くらいの大きさだから、進む長さも2倍になると思います。
2倍の大きさとは、どういうことですか。
直径の長さが2倍くらいあるという意味です。
円の大きさとは、直径の長さのことなのですね。○○さんは、直径の長さが2倍になると、進む長さも2倍になると予想しましが、みなさんは、どう思いますか。
長くはなると思うけれど、きっちり2倍になるのかな。
それでは、試してみましょう。(実際に転がしてみせる。)
いくつもの円盤の結果について考える
いくつもの円を転がしていくと、次のような図ができてきます。直径の頂点を直線で結ぶと、比例のグラフのようになります。子供たちに、これを見て気付いたことを尋ねます。
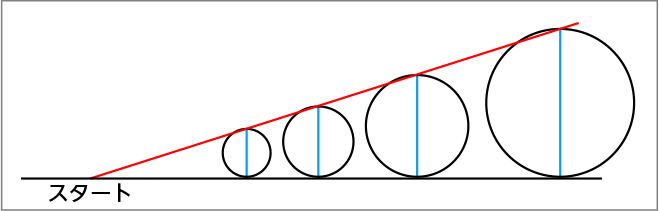
この図を見て、気付いたことはありますか。
直径の長さが2倍、3倍……になると、円周も2倍、3倍…になっています。
そういう関係を何と言いましたか。
比例です。直径と円周は、比例の関係になっています。
そうですね。それでは、円周の長さは直径の何倍になっていますか。
円周は、直径の3倍になっています。
大きい円でも小さい円でも、3倍という割合は一緒です。
本当にそうですか。
比例しているのだから、直径と円周の割合は同じはずです。
でも、3倍よりはちょっと長い気もするよ。
ぴったり3倍かどうか確かめてみないと分からないよ。
それでは、実際に測って確かめてみましょう。
このように、円の大きさ(直径)と1回転で進む長さ(円周)には、比例の関係があることを確かめたうえで、「円周は直径の何倍でしょう」と子供たちに尋ねます。
見た目から、大体3倍くらいだということは予想がつくことでしょう。答えの見通しがもてたところで、実際に円周が直径の何倍なのかを調べていきます。

円周と直径の関係を調べよう。
見通し
- 直径が大きくなればなるほど、円周も大きくなる。
- 直径が2倍、3倍、4倍……になれば、円周も2倍、3倍、4倍……になる。
- 直径と円周は比例していると言えそう。
- どんな大きさの円も、円周の長さは直径の長さの大体3倍。
自力解決の様子
自力解決の前に、直径の測り方や円周の測り方をしっかりと確認しておきましょう。うまく測定できない子供には、「円周を測る巻き尺がねじれている」「直径を測る際に円を垂直に挟めていない」などのつまずきが予想されます。机間指導しながら、声をかけていくとよいでしょう。
A つまずいている子
・円周が直径の約3倍になっていることを予想している。
円周を測る巻き尺がねじれている、直径を測る際に垂直に挟めていないなどして、測定がうまくいかない。
B 素朴に解いている子
・円周が直径の約3倍になっていることを確認している。
特定の円について調べ、結論を導き出している。
C ねらい通り解いている子
・どんな大きさの円でも円周が直径の3倍より少し大きい割合になっていることを確認し、さらに詳しい数値を調べようとしている。
さまざまな大きさの円を試して、結論を導き出している。
学び合いの計画
学び合いでは、それぞれが調べた結果には誤差が含まれていることを確かめ、誤差の補正を考え合いながら、どんな円でも円周は直径の約3.14倍になっていることを導いていきます。その際、結果だけでなく、結果から感じた思いも尋ねるとよいでしょう。
円周率には、アルキメデスを始め、数多くの数学者たちを魅了してきたロマンがあります。子供たちにも、知識を習得するだけでなく、そうした算数の楽しさを感じてもらえることが期待されます。
ノート例
A つまずいている子

B 素朴に解いている子

全体発表とそれぞれの考えの関連付け
全体発表では、それぞれが調べた結果を報告し合います。そして、どんな円でも、円周は直径の約3.14倍になっていることを確認していきます。
円周は直径の何倍になりましたか。
イラスト/横井智美、やひろきよみ

