小4算数「倍の見方」指導アイデア《基準量を求める計算》
執筆/横浜市立山下みどり台小学校教諭・青木真璃奈
監修/文部科学省教科調査官・笠井健一、島根県立大学教授・齊藤一弥

目次
単元の展開
第1時 何倍かを求める計算
▼
第2時 比較量を求める計算
▼
第3時(本時)基準量を求める計算
▼
第4時 差による比較と割合を使った比較
▼
第5時 まとめ・たしかめ
本時のねらい
数量の関係に着目し、的確に演算決定をするとともに、その根拠について図を用いて説明することができる。
評価規準
問題場面について、数量関係に着目して捉え、図を使って説明している。
本時の展開

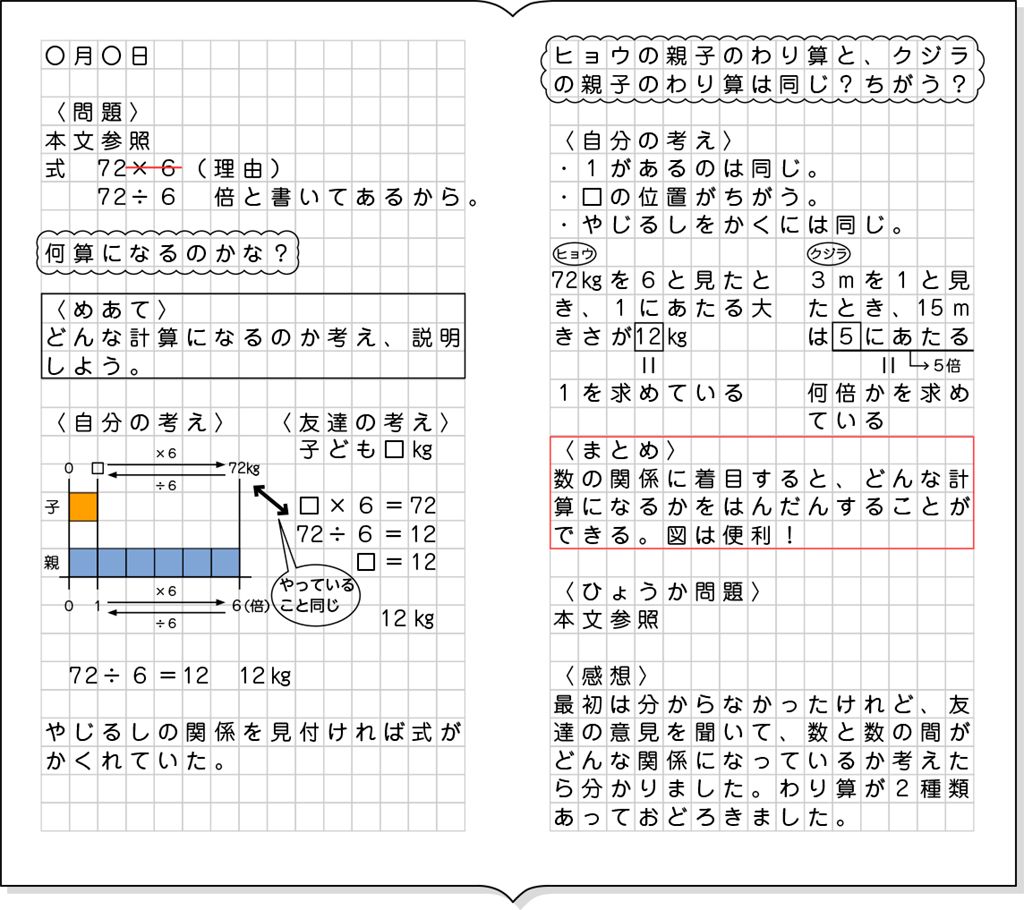
親のヒョウの体重は、子供のヒョウの体重の6倍で72㎏です。子供のヒョウの体重は何㎏ですか。
子供のヒョウの体重は何㎏か求められそうですか。
求められます。
すごいですね。何㎏ですか。
まだ計算できてないけれど、式は言えます。
そうですね。まずは式を教えてください。
72÷6です。
え、72×6でしょ。
あれ?どっちだろう。
意見が分かれましたね。
6倍と書いてあるから、かけ算じゃないのかな。
昨日とは問題が違う気がするよ。
うん。そもそも、親の体重より子供の体重のほうが軽いはずだから、わり算じゃないとおかしいよ。
なるほど。確かにそうかも。うーん。
では、子供のほうが親より体重が軽いはずだから、わり算なんですね。
それは、理由にならない気がします。だって、親より子供のほうが身長が高くなることもあるから、体重も子供のほうが重くなることがあり得ます。
確かに、絶対とは言い切れないかも。
もっと考えれば、何算なのか分かるはずだから時間が欲しい。
では、どんな計算になるのか、みんなで考えてみましょう。

どんな計算になるのか考え、理由を説明しよう。
見通し
三年生のわり算の学習で、□×2=6という式のときに、わり算を使って□を求めたな。(方法の見通し)
前回の学習のときに、数直線に数をあてはめて考えたよ。(方法の見通し)
親のヒョウの体重は、子供のヒョウの体重の6倍となっているから、親の体重のほうが重いはずだ。(結果の見通し)
自力解決の様子
A つまずいている子
問題の意味が捉えられず、□を使った式に表すことができずに困っている。
B 素朴に解いている子
□を使った式に表して、計算をしている。
C ねらい通り解いている子
式で表したことを図でも表し、数量の関係に着目して、わり算の式で表すことができる根拠を考えている。
学び合いの計画
問題文に「倍」と書いてあるからかけ算、答えが増えたらおかしいからわり算というように、感覚的に演算決定するのではなく、根拠をもって的確に演算決定する力を養いましょう。
演算決定をするためには、問題における数量の関係を的確に捉えることが必要であります。
そこで本時では、基準量、比較量、割合の3項の関係が捉えやすい図を用いて考察していくことを大切にしていきます。
また、第一用法のわり算と第三用法のわり算を比較することで、商の意味を割合の視点から捉え直します。
この問題場面の数量関係を図に表して構造的に捉える経験や、商の意味を割合の視点から捉え直す経験は、第5学年の小数のかけ算・わり算、単位量当たりの大きさ、割合の学習でも生かされていきます。
学び合いのなかで、式と図のつながり、図と言葉のつながりに目が向いている子や、わり算の商の意味に気付いている子を価値付け、2量の関係に着目することへ関心を高めていけるようにしていきましょう。
ノート例
A つまずいている子
B 素朴に解いている子
全体発表とそれぞれの考えの関連付け
※C1、C2のそれぞれが発表をする。
C1
子供のヒョウの体重を□㎏とすると、親のヒョウの体重はその6倍だから、□×6になる。親の体重が72㎏だから、□×6=72
三年生のときも□×2=6の□を求めるときに、6÷2をして求めたから、今回も同じように、72÷6をする。
72÷6=12だから、子供のヒョウの体重は12㎏になる。
C2
前回のように、図を使って考える。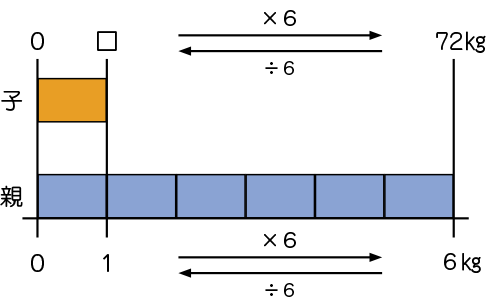
72÷6=12 12㎏
今回は何算ということがわかりましたか。
イラスト/横井智美