小6算数「分数のわり算」指導アイデア（1）
執筆／埼玉県公立北小学校教諭・松井浩司
編集委員／国立教育政策研究所教育課程調査官・笠井健一、埼玉県公立小学校校長・書上敦志
目次
本時のねらいと評価規準
（本時の位置 １／11）
ねらい
分数でわることの意味について考える。
評価規準
分数÷分数の立式の根拠を数直線や言葉の式を用いて考え、説明している。（数学的な考え方）
問題
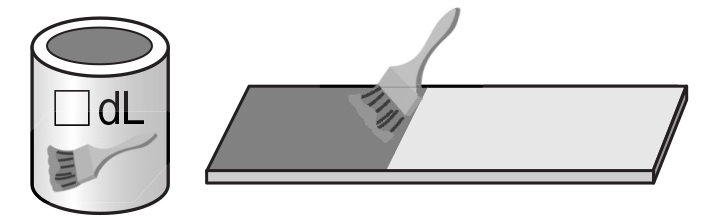
□がどんな数ならできますか。
２dL なら簡単にできる。
なるほど。でも、２だけじゃなくて、３とか４、……とかでもできると思う。
例えば、２dL ならどんな式になりますか。
２等分なので、[MATH]\(\frac{2}{5}\)[/MATH]÷２です。
では、[MATH]\(\frac{3}{4}\)[/MATH]dL では、どんな式になりますか。
[MATH]\(\frac{2}{5}\)[/MATH]÷[MATH]\(\frac{3}{4}\)[/MATH]になると思います。
÷[MATH]\(\frac{3}{4}\)[/MATH]って？ どういうことですか。
わる数が分数でもいいのかな？
どんな式になるのかな。
本時の学習のねらい
どんな式になるのか考え、その理由を説明しよう。
見通し
□に当てはまる数を考えさせることで、既習の学習（分数÷整数）を想起できるようにしていきます。その後、□の数を[MATH]\(\frac{3}{4}\)[/MATH]として、本時の学習内容を提示していきます。除数が整数の場合から導入することで、除数が分数に変わっても、同じように立式できると見通しを持たせます。そして、既習との関連を捉えさせた上で、[MATH]\(\frac{2}{5}\)[/MATH]÷[MATH]\(\frac{3}{4}\)[/MATH]の式で本当によいのか、と子供に問い、自力解決へとつなげていきます。
なお、立式の根拠として数直線を活用していくことが大切です。子供の実態によっては復習として、÷整数の場合の数直線をつくる活動を振り返っておくとよいでしょう。
自力解決の様子
A つまずいている子
・誤答。立式の理由を書くことができない。
・[MATH]\(\frac{2}{5}\)[/MATH]÷[MATH]\(\frac{3}{4}\)[/MATH]
・[MATH]\(\frac{3}{4}\)[/MATH]÷[MATH]\(\frac{2}{5}\)[/MATH]
B 素朴に解いている子
・整数の場合から言葉の式に整理して説明している。
ぬった面積÷使った量＝１dL でぬれる面積
C ねらい通りに解いている子
・数直線に関係を整理し、比例関係から立式を説明している。
学び合いのポイント
イラスト／横井智美
『小六教育技術』2018年6月号より
