小6算数「円の面積」指導アイデア（1）

執筆／埼玉県公立小学校教諭・秋山泰孝
編集委員／国立教育政策研究所教育課程調査官・笠井健一、埼玉県公立小学校校長・書上敦志

本時のねらいと評価規準

（本時の位置　1／6　単元の導入）

ねらい
既習の図形の面積の求め方を基に、円の面積の求め方を考えることができる。

評価規準
円の性質に着目し、既習の図形の面積の求め方を基に円のおよその面積を考え、説明している。（数学的な考え方）

問題

（正方形、長方形、平行四辺形、台形、ひし形、三角形、円を提示する）

（問題を提示する）

（方眼紙に描かれた半径10㎝の円を提示する）

本時の学習のねらい

方眼の数の数え方を工夫して、円のおよその面積を求めよう。

見通し

円の図形的な特徴を問題解決に生かせるよう円を観察し、円はどのような図形かを話し合う時間をとります。その中で、円は対称な図形であり、半分に1 回、2 回と折ってもぴたりと重なり、合同な扇形ができることに気付かせていきます。また、曲線部分の方眼の数をどう数えればよいかを問い、平均して1つ0.5㎠として数えればよいことを全体でおさえ、自力解決に入るようにします。

自力解決の様子

方眼紙に半径10㎝の円を描いたプリントを子供に配付します。

A　つまずいている子

円全体の方眼を数えようとしている。

B　素朴に解いている子

[MATH]\(\frac{1}{4}\)[/MATH]や[MATH]\(\frac{1}{4}\)[/MATH]の円で考え、方眼の数を数えている。

C　ねらい通りに解いている子

正方形や直角三角形に着目し、計算で方眼の数を求めている。

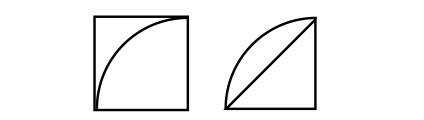
学び合いの計画

子供なりに考えた方眼の数の数え方のよいところを認め、よりよい考えへと高めていくようにします。ここでは、子供の考えと円の図形的な特徴とを関連付けていくことが大切です。

Ｂの考えのように扇形の面積を求め、倍積して円全体の面積が求められるのはどうしてかを問い、円の特徴を生かし手際よく面積を求めていることに気付くようにします。

また、C の考えのように、面積を求めることのできる既習の図形を見いだし、計算で面積を求められる部分とそうでない部分を分ける方法のよさにも触れたいものです。その中で、円を決定する要素である半径の数値を使っていること、円を等分する数を増やしていくと、扇形の中に見いだした三角形と弧との隙間が徐々になくなっていくことにも気付かせたいところです。

【本時の子供のノート例】

全体発表とそれぞれの考えの関連付け

C1の考え方

[MATH]\(\frac{1}{4}\)[/MATH]の円で考える。

C2の考え方

[MATH]\(\frac{1}{8}\)[/MATH]の円で考える。

C3の考え方

[MATH]\(\frac{1}{4}\)[/MATH]の円で考える（直角三角形に着目し、計算で求める）。

学習のねらいに正対したまとめ

円の特徴を生かし、等分して合同な形に着目すると、計算を用いて手際よく面積を求められる。

評価問題

子供に期待する解答の具体例

三角形の面積　10 × 7 ÷ 2 ＝ 35
△の方眼の数　11 ÷ 2 ＝ 5.5
（35+5.5）× 8 ＝ 324

本時の評価規準を達成した子供の具体の姿

[MATH]\(\frac{1}{8}\)[/MATH]の円の中に三角形を見いだし、計算を用いて円のおよその面積を求めることができる。

次時につながる感想例

ワンポイント・アドバイス

埼玉県さいたま市立大砂土小学校校長・書上敦志

本単元は、曲線で囲まれた図形の面積を工夫して測定する能力を伸ばすとともに、円の面積を求める公式をつくる活動から、算数として簡潔かつ的確な表現へと高める能力を伸ばすことをねらいとしています。

本単元の導入である第１時では、既習の学びを基に、これまでに同じような似たような問題がなかったか、また、どのように解決してきたか、どのように考えてきたかといった、これまでの学び方を振り返ることが大切です。正方形、三角形、平行四辺形などの基本図形の求積公式、図形の対称性、概形とおよその面積などの学習内容を振り返り、広い視野から総合的に問題解決に役立ちそうな知識を想起し、手際よい解決方法を話し合っていきます。

イラスト／横井智美

『小六教育技術』2018年5月号より

■6年算数　円の面積（2）