小6算数「データの活用」指導アイデア
執筆/埼玉県公立小学校教諭・齋藤礼乃
編集委員/文部科学省教科調査官・笠井健一、浦和大学教授・矢部一夫
目次
本時のねらいと評価規準
(3時間を通して1つの問題に取り組みます。本時は3/3時)
ねらい
目的に応じたデータから、データの特徴や傾向を分析し、問題に対する結論について、根拠をもって考察することができる。
評価規準
家族にお願いするおこづかいの金額をいくらにすればよいか、その根拠を表やグラフから考えることができる。
前時まで
第1時、第2時では、「翔平さんも毎月おこづかいをもらえるようになりました。いくらもらうように家の人にお願いすればよいでしょう。」という問題場面を提示し、友達がもらっているおこづかいの金額を調べ、平均値や中央値、最頻値などを求めたり、度数分布表や柱状グラフを作成したりしました。
問題場面
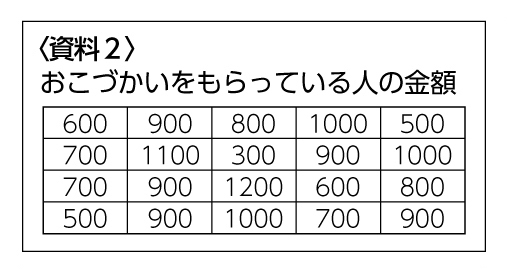
クラスのみんなのおこづかいを調べると、このような結果でした。
翔平さんは、いくらおこづかいをもらうようにお願いすればよいでしょう。
本時
前回の授業では、集めたデータを数値に表したり、表やグラフにまとめたりしました。
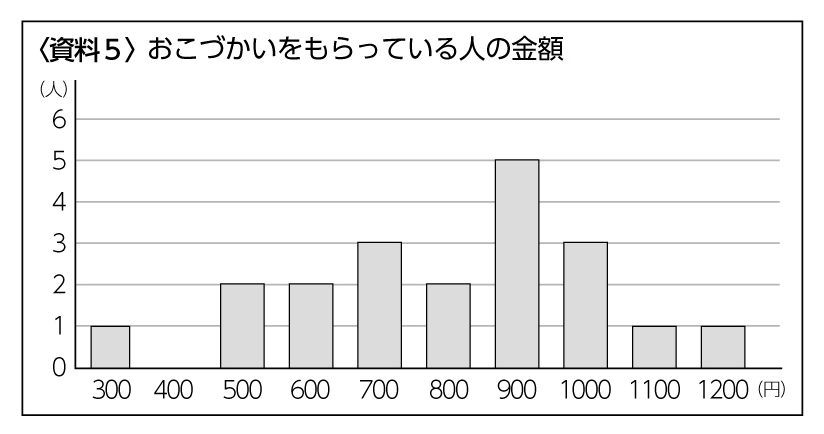
おこづかいの金額に散らばりがありました。一番多い人と少ない人では、900円も差がありました。(資料5)
一番多くの人がもらっている金額は、900円でした。(資料4、5)
今日はこのデータをもとに、翔平君が家の人にいくらもらえるようにお願いすればよいか、考えていきます。
おこづかいをもらっていない人については、どうすればいいですか。
前回と同様に、おこづかいをもらっている人のデータを使って考えましょう。
本時の学習のねらい
家の人にお願いするおこづかいの金額と、その理由を考えよう。
見通し
- どの資料が使えそうかな。
- おこづかいの金額の値の資料が使えそうです。平均を使って考えてみよう。
- 度数分布表や柱状グラフなら、どの金額が一番多いか一目で分かるので、家の人にうまく伝えられると思う。
自力解決の様子
A つまずいている子
たくさんある資料の中からどれを使えばよいか分かっていない。
B ねらいどおりに解決している子
クラスのおこづかいの平均は800円だから、800円がよいと考えている。
C 進んでいる子
最頻値や中央値、おこづかいをもらっていない子も含めた平均を求めるなど、様々なデータを活用して考えている。
学び合いの計画
イラスト/横井智美
『教育技術 小五小六』2021年12/1月号より