小6算数「拡大図と縮図」指導アイデア
執筆/埼玉県公立小学校教諭・清水武蔵
編集委員/国立教育政策研究所教育課程調査官・笠井健一、埼玉県公立小学校校長・書上敦志
目次
本時のねらいと評価規準
(本時の位置7/8)
ねらい
縮図を描いて、実際の長さを求めることができる。
評価規準
・直接測れない長さを求めるには、縮図を用いればよいことに気付き、用いようとしている。(関心・意欲・態度)
・直接測ることのできない長さを、縮図を描いて求めることができる。(技能)
問題
下の図は、はるかさんが校舎から10mはなれた所に立って、校舎の上はしAを見上げている様子を表したものです。下の図の校舎の実際の高さは、何mですか。
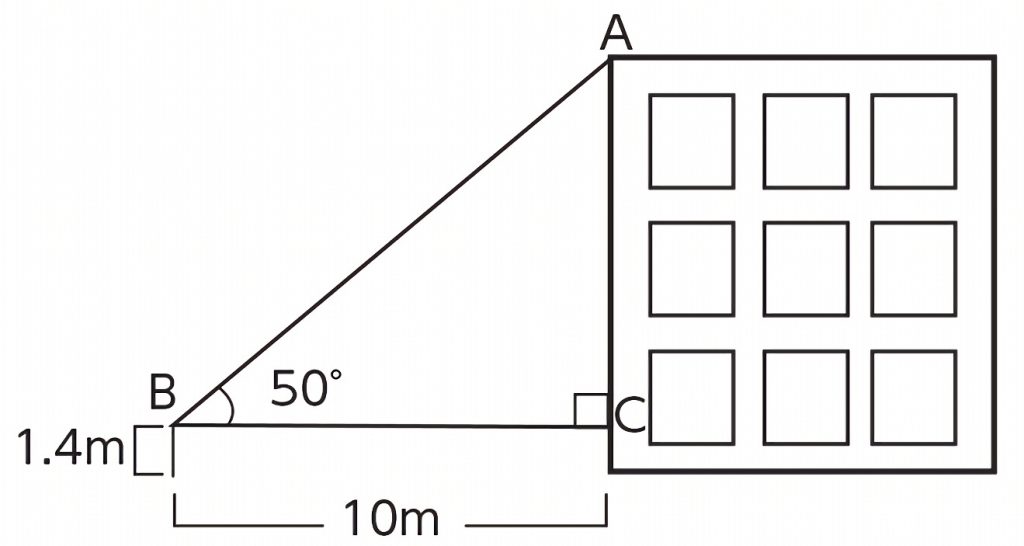
実際に測ることはできますか。
直接は測れない。難しいと思います。
どのようにすれば、高さを求めることができますか。
前の時間みたいに、縮図を描けばできそうです。
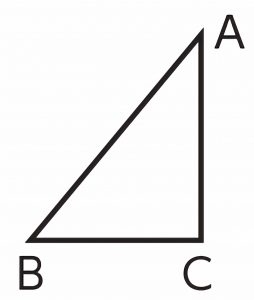
点A、点B、点Cを三角形と見て、縮図にします。
どの部分が高さになっていますか。
辺ACが高さになっています。
どのくらいの縮尺がよさそうですか。
[MATH]\(\frac{1}{100}\)[/MATH] はどうかな。
[MATH]\(\frac{1}{200}\)[/MATH] なら、あまり大きくならなくて描けそう。
[MATH]\(\frac{1}{100}\)[/MATH] や [MATH]\(\frac{1}{200}\)[/MATH] の縮尺で縮図を描いて、高さを求めましょう。
本時の学習のねらい
直接測れない長さを、縮図を描いて求める方法を考えよう。
見通し
問題提示の後に、実際に測れない場合は、どのようにして求めるかを話し合います。今回の問題では、点A、点B、点Cを頂点とする三角形ABCとして見て、縮図を描いて求める方法を考えることを課題とします。 前時までに縮尺を学習しているので、縮尺をどのくらいにするかについても触れるとよいでしょう。今回は、 [MATH]\(\frac{1}{100}\)[/MATH] と [MATH]\(\frac{1}{200}\)[/MATH] の縮尺で自力解決できるようにしています。
自力解決の様子
A つまずいている子
・縮図を描く際に、辺BCの10mを何㎝にすればよいか分からない。
・縮図をどのように描くかが分からない。
・1.4mを足していない。
B 素朴に解いている子
[MATH]\(\frac{1}{100}\)[/MATH] の縮図を描いて解いている。
・辺BC= 10㎝
・角B= 50°
角C= 90°
・頂点Aと頂点Cを結び長さを測る。
・辺AC=約12㎝
・12 × 100 = 1200
1200㎝= 12m
12m
・12 + 1.4 = 13.4
約13.4m
C ねらい通りに解いている子
長さに合わせて縮尺を選び、考え方を説明している。
辺BC=5㎝になって描きやすいので、[MATH]\(\frac{1}{100}\)[/MATH] の縮尺で考えました。
角B= 50°、角C= 90°、頂点Aと頂点Cを結び、長さを測ると、辺AC=約6㎝なので、
6× 200 = 1200
1200㎝= 12m
12m
12 + 1.4 = 13.4
約13.4m
学び合いの計画
イラスト/横井智美
『小六教育技術』2018年9月号より