小4算数「分数」指導アイデア《同分母の帯分数のひき算》

執筆/富山大学人間発達科学部附属小学校教諭・屋鋪善祐
監修/文部科学省教科調査官・笠井健一、前・富山県南砺市立福光東部小学校校長・中川愼一

目次
単元の展開
第1時 真分数・仮分数・帯分数の表し方や意味を理解する。
▼
第2時 数直線や単位分数に着目し、仮分数や帯分数で表わす。
▼
第3時 仮分数を帯分数に直す方法を考える。
▼
第4時 帯分数を仮分数に直す方法を考える。
▼
第5時 異分母分数の大小関係について考える。
▼
第6時 同分母の分数のたし算・ひき算のしかたを考える。同分母の「真分数+真分数(くり上がりあり)」、同分母の「仮分数-真分数」
▼
第7時 同分母の帯分数のたし算のしかたを考える。同分母の「帯分数+帯分数(くり上がりなし)」、同分母の「帯分数+帯分数、帯分数+真分数(くり上がりあり)」
▼
第8時(本時)同分母の帯分数のひき算のしかたを考える。同分母の「帯分数-帯分数、帯分数-真分数(くり下がりあり)」
本時のねらい
同分母の帯分数のひき算(くり下がりあり)のしかたについて、既習の同分母の帯分数のたし算(くり上がりあり)を基に考える。
評価規準
くり下がりのある同分母の分数のひき算のしかたを、単位分数の数に着目して考えている。(思考・判断・表現)
本時の展開

次の計算をしましょう。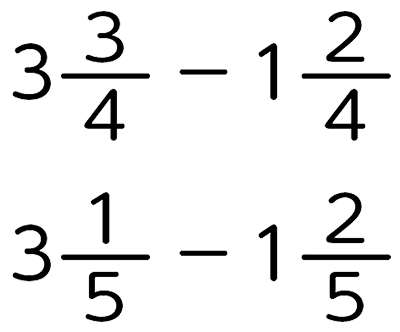
次の計算をしましょう。「3[MATH]\(\frac{3}{4}\)[/MATH]-1[MATH]\(\frac{2}{4}\)[/MATH]」
前の時間に学習した帯分数のたし算のときのように、整数どうし、分数どうしで計算すればできるはずです。
3-1=2、[MATH]\(\frac{3}{4}\)[/MATH]-[MATH]\(\frac{2}{4}\)[/MATH]=[MATH]\(\frac{1}{4}\)[/MATH]なので、答えは2[MATH]\(\frac{1}{4}\)[/MATH]です。
それでは、次の計算はどうでしょう。「3[MATH]\(\frac{1}{5}\)[/MATH]-1[MATH]\(\frac{2}{5}\)[/MATH]」
さっきと同じように、整数どうし、分数どうしで計算すればできるはずだよ。
あれ……。でも[MATH]\(\frac{1}{5}\)[/MATH]-[MATH]\(\frac{2}{5}\)[/MATH]をすると、引く数のほうが大きいから計算できない。どうすればいいのかな。
分数どうしが引けない計算ですね。どのように計算すればよいと思いますか。
分数どうしで計算できるように、分数の形を変えればいいと思います。
分数を変形すれば計算できそうです。

分数どうしが引けない場合の計算のしかたを考えよう。
見通し
整数の部分から1をくり下げて、分数([MATH]\(\frac{5}{5}\)[/MATH])に直せば計算できるはずだ。(方法の見通し)
帯分数を仮分数に直せば、[MATH]\(\frac{1}{5}\)[/MATH]の何個分と見ることができるから計算できるはずよ。(方法の見通し)
これまでのように、単位分数のいくつ分という考えは使えるはず。(結果の見通し)
自力解決の様子
A つまずいている子
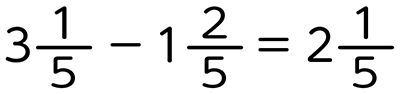
分数どうしのひき算がうまくできず、正しい計算ができていない。
B 素朴に解いている子
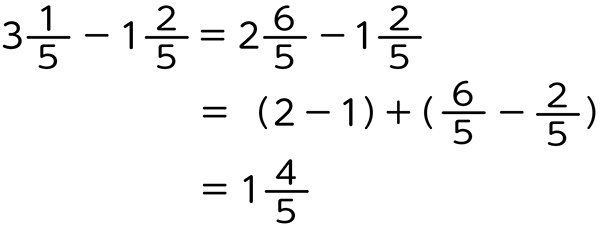
整数の部分からくり下げて3[MATH]\(\frac{1}{5}\)[/MATH]を2[MATH]\(\frac{6}{5}\)[/MATH]に直し、整数どうし、分数どうしで計算している。
C ねらい通り解いている子
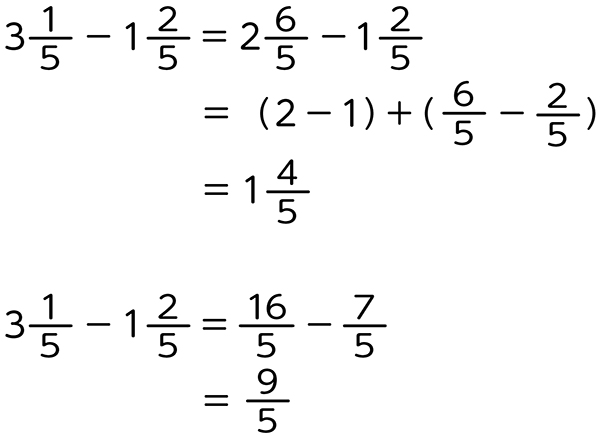
整数の部分からくり下げて、整数どうし、分数どうしで計算する方法を考えている。また、帯分数を仮分数に直す方法を見いだしている。そして、それぞれの考えのよさに気付いている。
学び合いの計画
第4学年「同分母の分数のたし算・ひき算」の単元では、1より大きい分数や大きさの等しい分数について理解し、分数のたし算・ひき算の計算の方法について考え、その計算ができる力を養うことが大切です。
イラスト/横井智美

