小4算数「面積」指導アイデア《長方形を組み合わせた図形の面積の求め方》
執筆/富山県高岡市立能町小学校教諭・本間大輔
監修/文部科学省教科調査官、笠井健一、前・富山県南砺市立福光東部小学校校長・中川愼一

目次
単元の展開
第1時 図形を構成する正方形や長方形の数に着目し、面積の比べ方を考える。
▼
第2時 面積の意味、単位「平方センチメートル(㎠)」を知る。
▼
第3時 1㎠のますの数に着目し、長方形や正方形の面積を求める公式を考える。
▼
第4時 面積の公式を適用して、面積を求める。
▼
第5時(本時)長方形を組み合わせた図形について、構成する長方形、正方形に着目し、面積の求め方を考える。
▼
第6時 基にする広さに着目して、大きな面積の表し方を考える。
▼
第7時 1m=100㎝であることに着目し、1㎡=10000㎠であることを考える。
▼
第8時 面積の単位「アール(a)」「ヘクタール(㏊)」「平方キロメートル(㎢)」を知る。
▼
第9時 正方形の1辺の長さに着目し、単位の相互関係を考える。
▼
第10時 表や折れ線グラフに着目して、縦の長さと面積の関係を考える。
▼
第11時 学習内容の習熟や定着、数学的な見方・考え方のふり返りを行う。
本時のねらい(長方形・正方形の面積の公式を学習した後)
長方形を組み合わせた図形について、既習の長方形や正方形の面積の公式を使えるように工夫し、面積を求める方法を考える。
評価規準
長方形を組み合わせた図形について、いくつかの長方形で構成されていることに着目して、その図形の面積の求め方を考えている。(思考・判断・表現)
本時の展開

下の図形の面積は何㎠でしょう。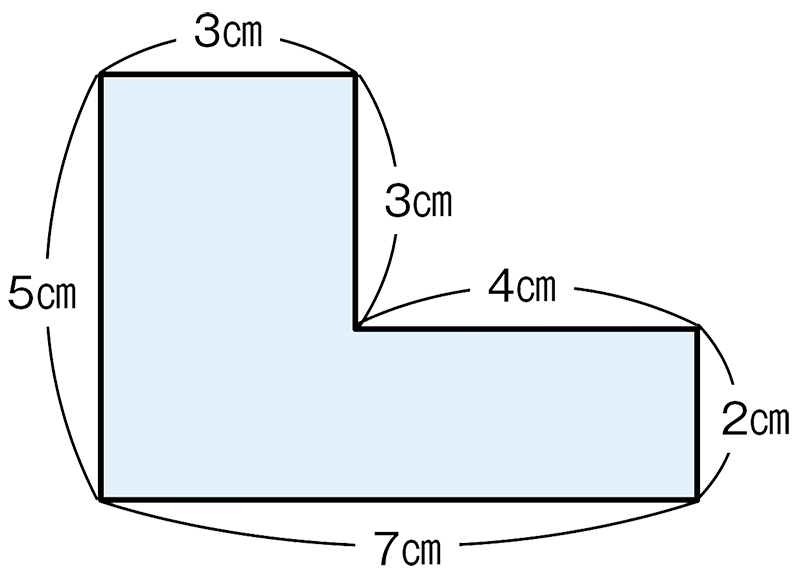
この図形の面積は、何㎠でしょう。
えー。ちょっと難しそうです。
どんなところが難しそうですか。
長方形か正方形だったら、面積を求める公式が使えるんだけど……。
皆さんは長方形や正方形なら公式を使って面積を求められるんですね。この図形に、長方形や正方形の面積の公式を使うことができないかを考えてみましょう。
一度に求めないで、長方形や正方形に分けて考えればよいのではないかな。
線を引いたら2つの長方形に分けられます。
長方形なら、面積の公式が使えます。
小さい長方形を付け足したら、大きい長方形になります。
大きい長方形の面積から、付け足した小さい長方形の面積を引いたら、求められそうです。
なるほど。長方形や正方形の面積の公式を使うための工夫ができそうですね。それでは、長方形の面積の公式を使うための工夫を考えていきましょう。できる人は、どのような工夫をしたのかが分かるように、図や式、言葉を使って表すことも考えてみましょう。

面積の公式を使えるようにするための工夫を考えよう。
見通し
長方形や正方形を作れば、面積の公式を使って面積を求められそうだ。(方法の見通し)
線を引いて長方形や正方形に分ければよい。(結果の見通し)
大きい長方形と見て、付け足した分の小さい長方形を引けばよい。(結果の見通し)
自力解決の様子
A つまずいている子
マス目の数から、面積が23㎠ということは分かるが、長方形や正方形に分けて考えることまではできていない。
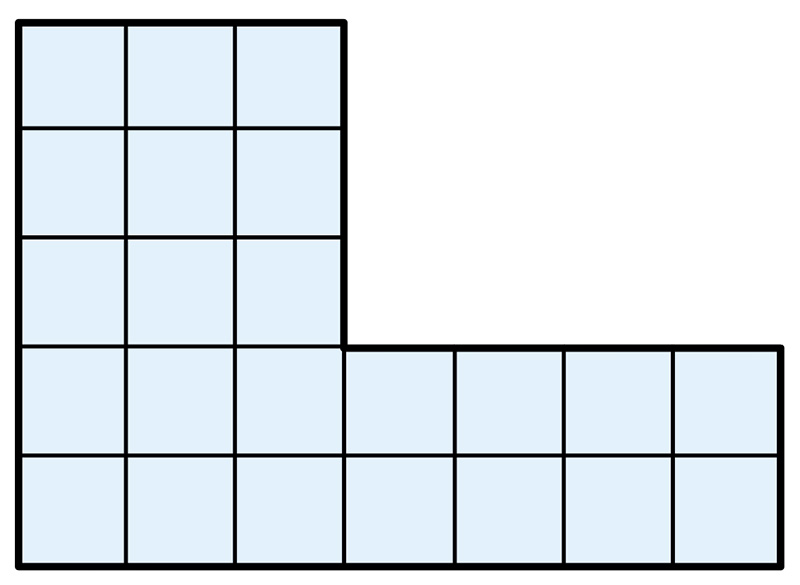
正方形が23個だから、23㎠
B 素朴に解いている子
図形の中に長方形や正方形を見いだし、インフォーマルな方法で23㎠であることを導き出しているが、面積の求め方を筋道立てて整理するまでには至っていない。
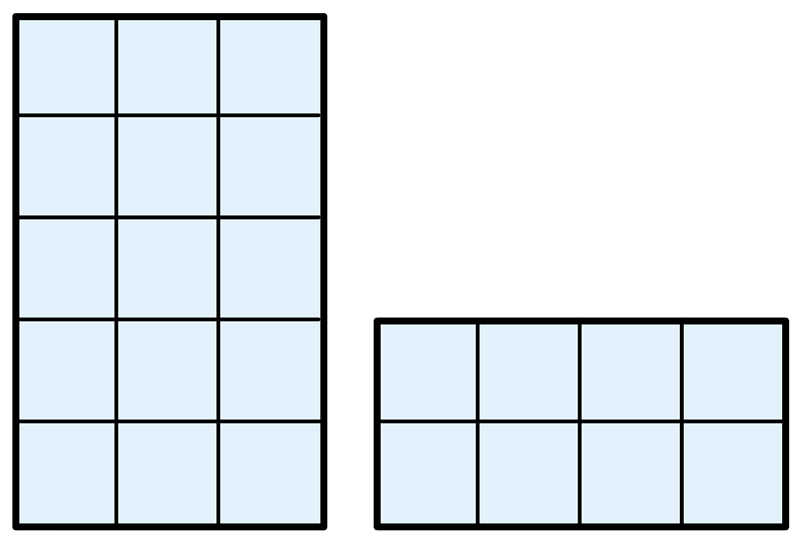
15+8=23 23㎠
C ねらい通り解いている子
長方形や正方形の面積の公式を使う工夫を明らかにして、それを図や式、言葉で整理している。
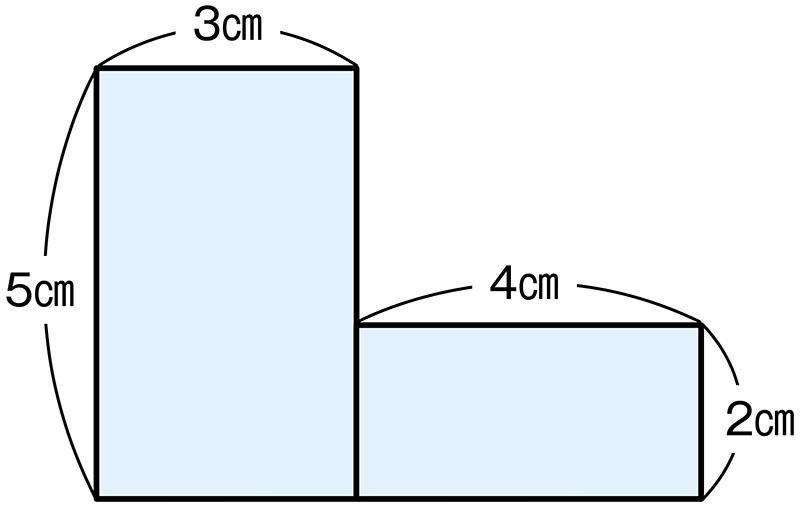
5×3+2×4=15+8=23 23㎠
学び合いの計画
この学習では、まず、学習した長方形や正方形の面積の公式が使えそうかを全体で考えます。
そのなかで、子供たちの発言から、分割すれば長方形が2つになることや、大きい長方形から小さい長方形を引くとよいことなどの子供の気付きを学級全体で共有し、価値付けていくことが大切です。このような図形の見方をすることで、既習の公式が使えそうだという解決方法の見通しをもたせるようにします。
イラスト/横井智美

