小6算数「拡大図と縮図」指導アイデア
執筆/埼玉県公立小学校教諭・小田木香純
編集委員/文部科学省教科調査官・笠井健一、浦和大学教授・矢部一夫
目次
本時のねらいと評価規準
(本時1/8時)
ねらい
拡大図、縮図の意味や性質について調べ、説明することができる。
評価規準
図形を構成する要素及び図形間の関係に着目し、合同の意味を基に、拡大図や縮図の意味を考えている。
問題場面
○○小学校のシールを作ります。同じ形のまま大きくして目立たせたいと思います。
私たちの小学校のシールをもう少し大きくして同じ形のまま目立たせたいと思います。
大きくしますね。(横の長さを2倍にした(い)を提示する)
え? 待ってください。違います!
大きくしたんだけれど、何が違うの?
横に広がってしまって、もとのシールの形と違います。
そうですか。では、どうしたらいいですか。
縦に長くしてください。
縦に長くしますね。(縦の長さを2倍にした(う)を提示する)
え? 今度は縦に伸びてしまってもとの形と違います。
横に広げたり、縦に長くしたりしましたが、形が変わってしまいましたね。同じ形は作れないのでしょうか。
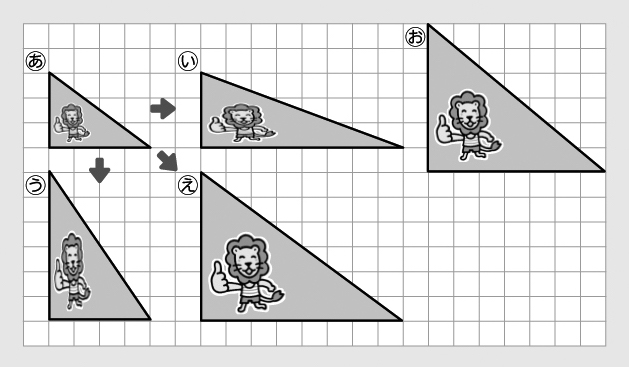
C1:横にも縦にも3マスずつ伸ばしたらどうかな。〔(え)〕
C2:横に2倍、縦にも2倍に伸ばしたらできるんじゃないかな。〔(お)〕
なるほど。C1さんとC2さんのように、横も縦も同じように伸ばしてみたら、同じ形のまま大きくできるというのですね。(C1とC2の反応を取り上げ、全体に提示する)
(え)は同じ形に見えるけれど違うみたいだなぁ。
(お)は(あ)と同じ形だと思います。
では、(お)が同じ形に見えるわけを考えましょう。
本時の学習のねらい
(あ)と(お)が、大きさは違っても同じ形に見える理由を考えよう。
見通し
図形のどこに注目して調べたらいいかな。
合同な図形の時に辺の長さに着目したので、対応する辺の長さに注目して調べてみよう。
合同な図形は角の大きさが同じだったので、対応する角の大きさに注目して調べてみよう。
自力解決の様子
A つまずいている子
辺の長さや角の大きさを調べた後、どうしたらよいか分からない。
B 辺の長さの関係に気付かない子
角の大きさは等しいんだけれど、辺の長さの関係はどうなっているんだろう。
C ねらい通り解いている子
対応する角の大きさがすべて等しく、辺の長さがどれも2倍になっている。
学び合いの計画
イラスト/横井智美
『教育技術 小五小六』2021年8/9月号より