小5算数「小数のわり算」指導アイデア《小数÷小数の計算のしかた》

執筆/福岡教育大学附属久留米小学校教諭・廣木伸幸
監修/文部科学省教科調査官・笠井健一、福岡教育大学教授・清水紀宏

目次
単元の展開
第1時 問題場面の数量の関係を数直線に表し、除数が小数の除法の意味を捉える。
▼
第2時 除法に関して成り立つ性質を使って、整数÷小数の計算のしかたを考える(除数が1より大きい場合)。
▼
第3時 除法に関して成り立つ性質を使って、整数÷純小数の計算のしかたを考える(除数が1小さい場合)。
▼
第4時(本時) 除法に関して成り立つ性質を使って整数の除法にし、小数÷小数の計算のしかたを考える。
▼
第5・6時 除法に関して成り立つ性質を使って整数の除法にし、小数で割る筆算のしかたを考える。
▼
第7時 被除数を変えずに除数の数を変えたときの商を比較し、除数と商の大きさの関係を理解する。
▼
第8時 除法に関して成り立つ性質を使って筆算し、あまりがある場合の小数で割る除法の計算のしかたを考える。
▼
第9時 除法に関して成り立つ性質を使って筆算し、商を概数で表す方法を知る。
▼
第10・11時 問題場面の基準量と比較量の関係を数直線に表し、倍を表す小数や比較量の求め方を考える。
▼
第12時 問題場面の基準量と比較量の関係を数直線に表し、基準量の求め方を考える。
本時のねらい
除法に関して成り立つ性質を基にして、小数÷小数の計算のしかたを考える。
評価規準
除法に関して成り立つ性質を用いて除数を整数にして、小数÷小数が計算できることを説明することができる。[思考・判断・表現]
本時の展開

3.4mの重さが7.14kgのパイプがあります。このパイプ1mの重さはなんkgですか。
今日の問題は、このような場面です。何を求める問題ですか。波線を引きましょう。また、問題を解決するために大切な数に○を付けましょう。(少し時間をとって)発表しましょう。

今日の問題では、パイプ1mの重さを求めます。
問題を解決するためには、「3.4m」の重さが「7.14kg」ということが大切です。
付け加えて、「1m」の重さを求めることも大切です。
それでは、問題を解決するために大切な数を、数直線にまとめましょう。(少し時間をとって)発表しましょう。
「3.4m」の重さが「7.14kg」なので、「3.4m」と「7.14kg」を縦に揃えて書きました。
大切な数をまとめた数直線
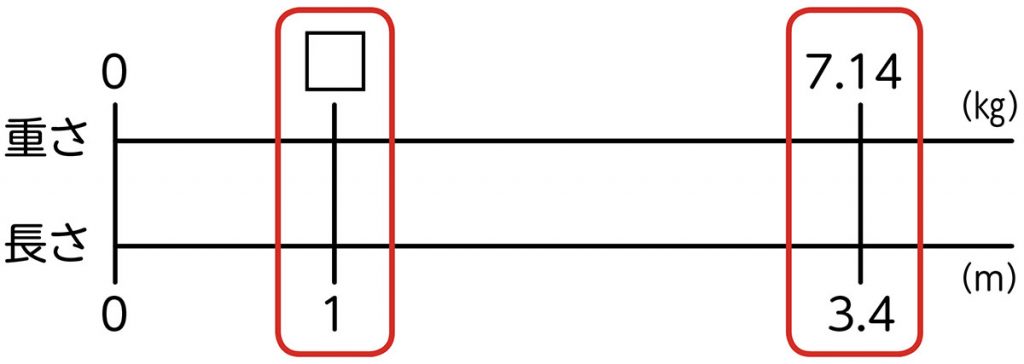
付け加えて、「1m」の重さが分からないので、「□kg」として、上の数直線のように「1m」と「□kg」を縦に揃えて書きました。
それでは、この□kgの求め方は、どのような式に表すことができますか。これまでの学習と同じように説明できますか。
3.4mは、1mの3.4倍です(矢印と×3.4をかき込む)。重さも□kgを3.4倍すると、7.14kgになります(矢印と×3.4をかき込む)。式でかくと、□✕3.4=7.14になります。□を求めるためには、7.14を3.4で割ります(矢印と÷3.4をかき込む)。式は7.14÷3.4だと思います。
立式のために書き込んだ数直線
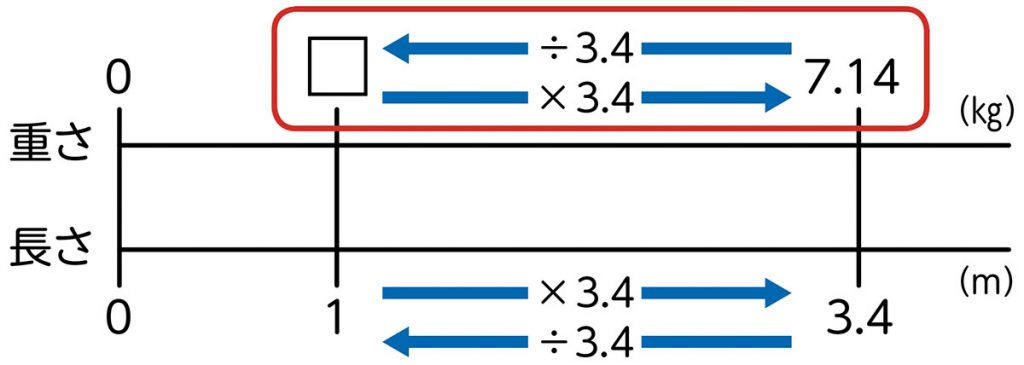
別の考えもあります。□✕3.4=7.14はかけ算だけど、かけ算とわり算は反対の計算なので、□を求める式は7.14÷3.4になります。
式に表すことができましたね。では、今日の問題と、前の時間の問題の、同じところや違うところは、どんなところですか。
【前時問題場面】
リボン2.4mの代金が96円でした。このリボン1mの値段はなん円ですか。
(式)96÷2.4
【問題場面】
3.4mの重さが7.14kgのパイプがあります。このパイプ1mの重さは何kgですか。
(式)7.14÷3.4
どちらも割る数が小数になっているのが同じです。
今日は小数÷小数の計算になっているのが違います。

小数÷小数の計算のしかたを考えよう。
見通し
- 数直線に表す〈方法の見通し〉
- わり算のきまりを使う〈方法の見通し〉
- 割られる数〈着眼の見通し〉
- 割る数〈着眼の見通し〉
- 商〈着眼の見通し〉
- 2㎏ぐらい〈結果の見通し〉
※前時で使った除法に関して成り立つ性質(わり算のきまり)を確認し、本時はこのきまりを基にして、計算のしかたを考えさせていきます。
自力解決の様子
A つまずいている子
わり算のきまりの理解が不十分であり、被除数と除数に違う数を掛けて計算し、商としている。

B 図を使って解いている子
わり算のきまりを用いて、除数も被除数にも100を掛けて、どちらも整数にしている。
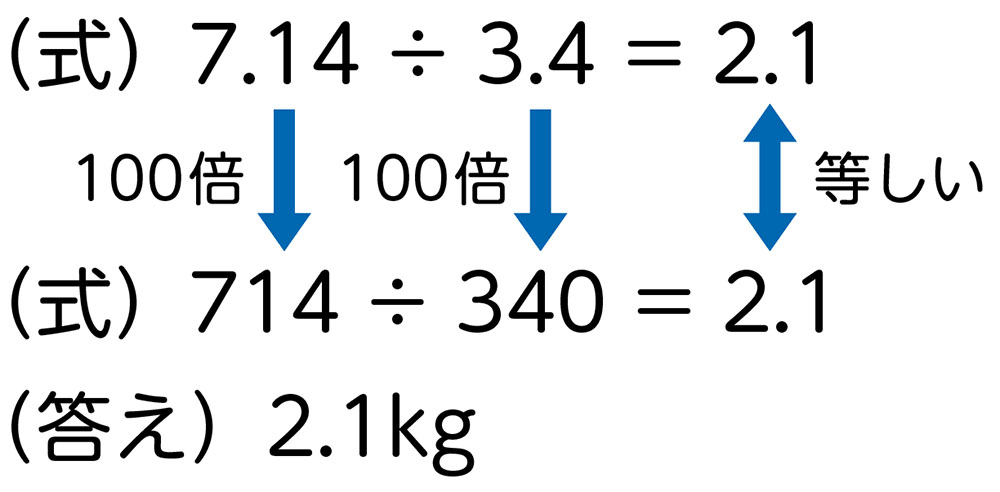
C ねらい通り解いている子
わり算のきまりを用いて、除数も被除数にも10を掛けて、除数を整数にしている。除数さえ整数になれば、計算できることに気付いている。
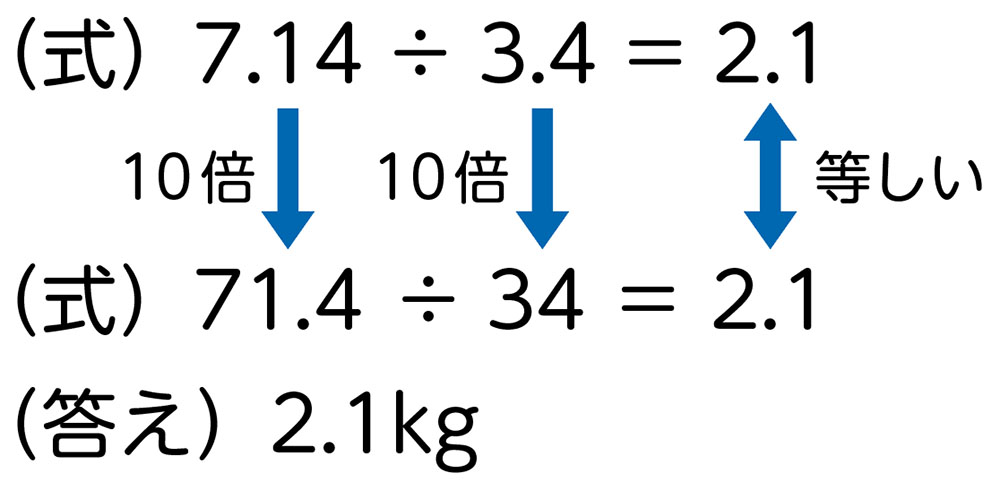
学び合いの計画
自力解決の段階で、1人1台端末を活用して、自他の解決方法を共有できるようにし、互いの解決方法を見合うことができるようにしておきます。
イラスト/横井智美

