小2算数「1000までの数」指導アイデア(10/12時)《数の大小関係/不等号を用いた式の表し方》
執筆/お茶の水女子大学附属小学校教諭・久下谷明
監修/文部科学省教科調査官・笠井健一、東京都目黒区立八雲小学校校長・長谷豊

目次
単元の展開
(1)数のあらわし方としくみ
第1時 3位数の読み方や表し方について考える。
▼
第2時 空位のある3位数の表し方について考えるとともに、数の仕組みに着目して3位数を書いたり読んだりする。
▼
第3時 数の仕組みに着目して、位取り板と数カードで数を表す。
▼
第4時 3位数の構成を基にした表し方(合成・分解)について考えるとともに、3位数の構成を等式で表す。
▼
第5時 1000未満の数について、数のまとまりに着目して、10を基にした数の相対的な大きさについて考える。
▼
第6時 数直線の読み取りを通して、3位数の大小や順序について考える。
▼
第7時 1000の構成と読み方、書き方について考えるとともに、1000付近の数についても考える。
▼
第8時 数の構成に着目して、1000までの数についていろいろな表し方を考える。
▼
(2)何十、何百の計算
第9時 10や100のまとまりに着目して、なん十±なん十、なん百±なん百などの計算のしかたを考える。
▼
(3)数の大小
第10時(本時)数の仕組みに着目して、数の大小関係について考え、不等号を用いて式に表す。
▼
第11時 数や式の意味に着目して、その大小、相関関係を不等号、等号を用いて式に表す。
▼
まとめ
第12時 学習内容の定着を確認するとともに、数学的な見方・考え方についてふり返る。
本時のねらい
数の仕組みに着目して数の大小関係について考え、不等号を用いて式に表すことができる。
評価規準
数の仕組みに着目して数の大小関係について考え、説明している。
不等号の意味を理解し、数の大小関係を不等号を用いて式に表すことができる。

今から、百の位まである二つの数を見せます。どちらが大きいでしょうか。
※下のように、最初は二つの3桁の数の上に画用紙などを被せて隠しておき、一の位から徐々に見せていきながら、問題を提示する。
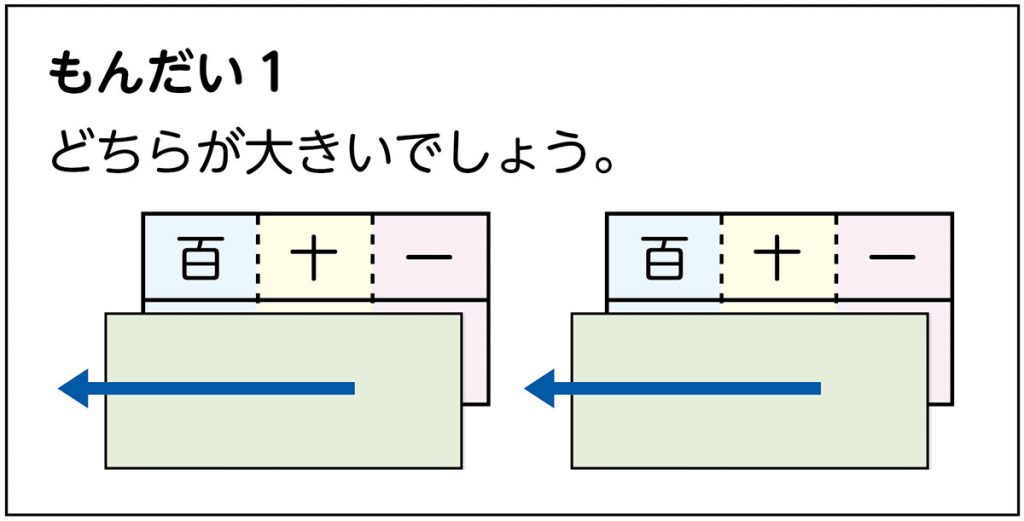
(百の位だけ隠れた状態で)どっちが大きいと思いますか。
左のほうが大きいです。
98と14だったら98のほうが大きいけど、百の位が数字が分からないから、まだ分かりません。
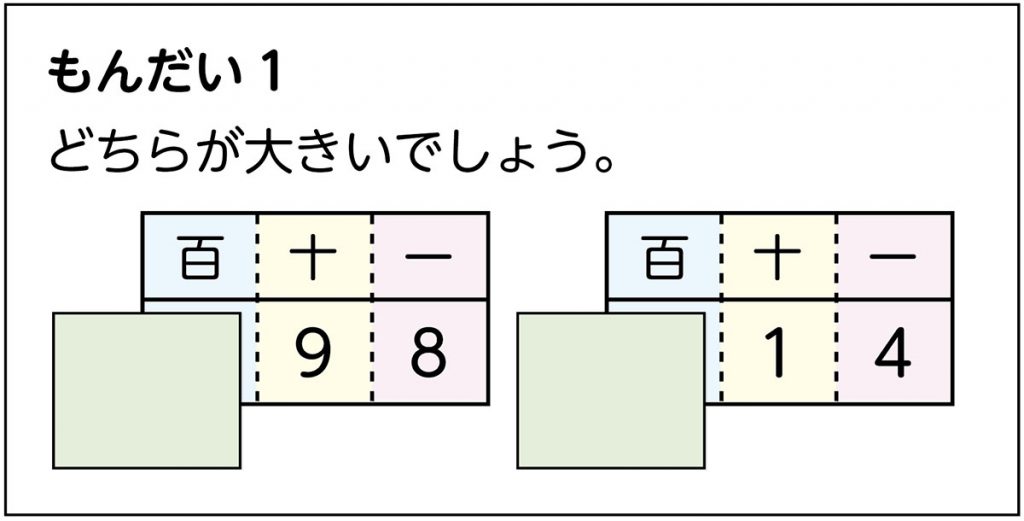
(全部を見せて)どちらが大きいか、分かりますか。

どちらが大きいかな。数の大きさのくらべ方を考えましょう。
見通し
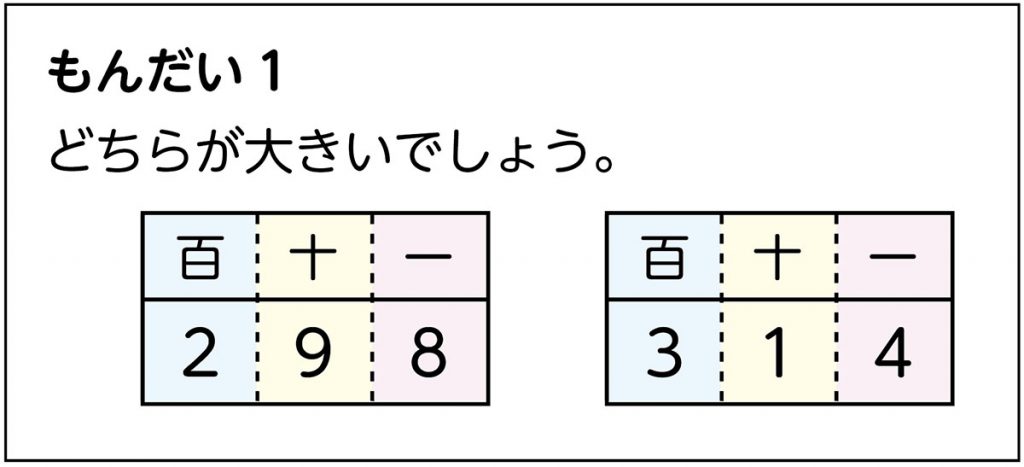
298と314では、どちらが大きいと言えそうですか。
314です。
314のほうが大きいと言えそうということですが、数の大きさを比べるには、数のどこを見て比べていけばよいでしょうか。数の大きさの比べ方を友達に説明できるように、ノートに書きましょう。
自力解決の様子
A つまずいている子
314のほうが大きいことは分かっているが、その理由を説明することができない。
B 素朴に解いている子
314のほうが大きいことは分かっていて、比べ方の説明として、“2と3をくらべる”とだけ書いている。
C ねらい通り解いている子
314のほうが大きいことが分かっていて、“(2と3を指し示して)一番大きい百の位の数字を比べる”と説明している。
学び合いの計画
どちらが大きいのか分かっていたとしても、その理由をどのように説明してよいのか戸惑い、止まってしまう子がいます。また、比べ方を話すことはできても、書くことが苦手で、どのようにノートに書いてよいのか悩んでいるような子もいます。
イラスト/横井智美

