小1算数「かたちづくり」指導アイデア《色板を使っていろんな形をつくってみよう》
執筆/富山大学人間発達科学部附属小学校教諭・屋鋪善祐
編集委員/文部科学省教科調査官・笠井健一、前富山県公立小学校校長・中川愼一
目次
本時のねらいと評価規準
[本時 2/5 : 直角二等辺三角形の色板でいろいろな形を構成する学習後]
ねらい
色板の形の特徴に着目し、具体的な操作を通して形の構成や分解について考える。
評価規準
色板をずらしたり回したり裏返したりして、形を構成したり分解したりすることを考えている。[数学的な考え方]

問題場面
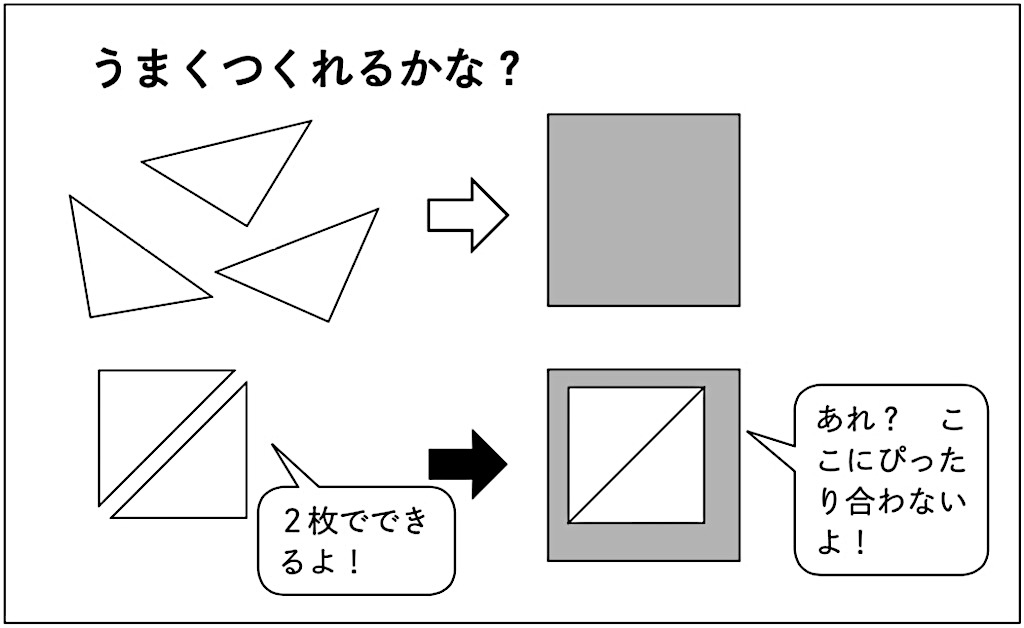
色板を使っていろんな形をつくってみましょう。この形をうまくつくることができますか?
できるよ! 簡単だよ! 2枚でできるよ。(操作)
では、当てはめてみましょう。(影絵に当てはめる)
ぴったり合わないのはどうしてかな?
わかった! 2枚じゃなくて、もっと多くの色板が必要なんだ!
4枚使えば、ぴったり合う真四角をつくれそうだよ。やってみたいな。
本時の学習のねらい
どうすれば、ぴったりの真四角の形をつくることができるのだろう?
見通し
前時までに、色板を使って、様々な形を作る活動を行っいます。本時は、つくる形を限定することによって、試行錯誤しながら図形の構成や分解について考える時間となります。直角二等辺三角形の色板を使って、いろいろな形をつくる活動を行います。色板を用いて形をつくる活動を行うことで、色板の位置や向き、組み合わせ方を変えると形が変わることに気付くことができます。実際に色板を動かしてみることによって、図形の構成や分解について着目できるようにします。さらに、自分の操作と友達の操作を比較する中で、「私と一緒!」「あれ、ぼくと違うな…」など、図形の構成や分解についての新たな発見が生まれます。
2枚で簡単につくることができる正方形ですが、4枚分の正方形を影絵で示すことによって、子どもたちに挑戦意欲が生まれます。「どうしてだろう?」「もっと色板を増やせばつくることができるかもしれない」と考える中で、同じ形でも色板の数によって大きさが異なることに気付くことができます。このような活動を十分に行い、図形の構成や分解について考える場を設けることで、図形についての感覚をより豊かにすることができます。
自力解決の様子
A つまずいている子
2枚を使った正方形はつくれるが、4枚の正方形をつくることができない。
4枚だと、どうやって真四角をつくるのかな…。
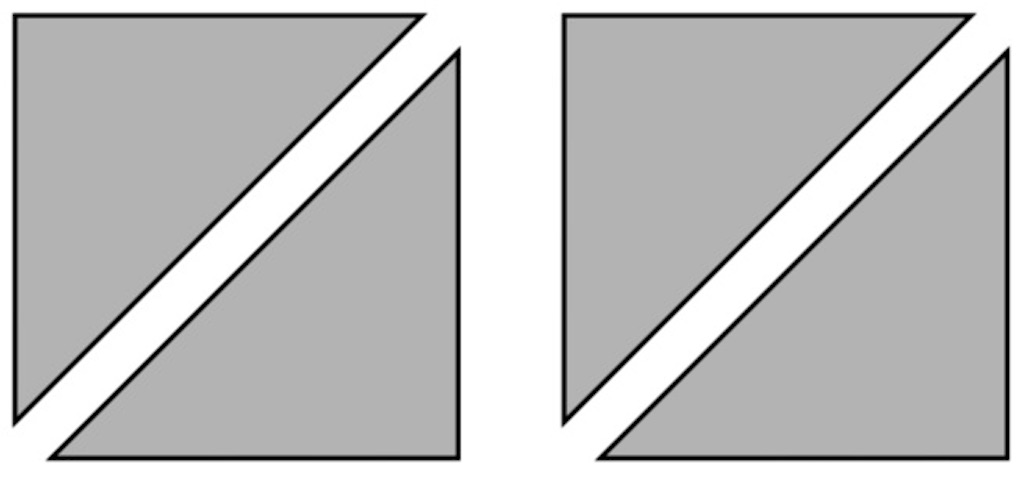
B 素朴に解いている子
色板の位置や向き、組み合わせ方を考え、4枚を使って正方形をつくることができる。
色板の向きを変えると、4枚の色板で真四角をつくることができたよ。
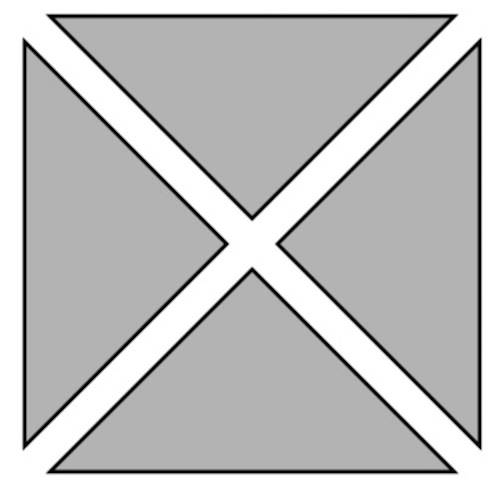
C ねらい通りに解いている子
色板の位置や向き、組み合わせ方を考えてつくったり、正方形の構成・分解の仕方に気付いて説明したりできる。
色板の向きを変えて、大きい三角を2つくっ付ければできるよ。
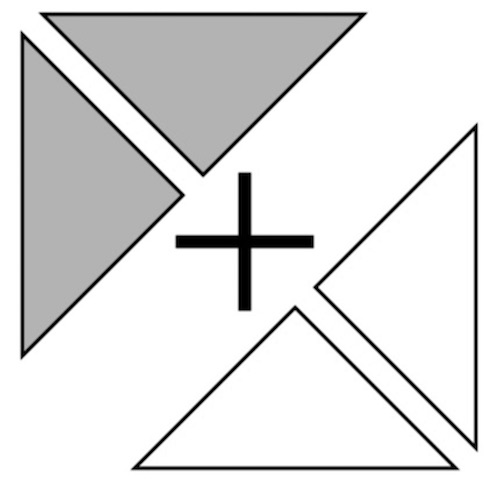
学び合いの計画
イラスト/コダシマアコ・横井智美
『教育技術 小一小二』2020年3月号より

