小5算数「整数の性質」指導アイデア
執筆/東京都公立小学校主任教諭・越後真紀
編集委員/文部科学省教科調査官・笠井健一、東京都公立小学校校長・長谷豊
目次
本時のねらいと評価規準
本時の位置 1/11 単元の導入
ねらい
乗法や除法に着目した観点で、整数を類別する仕方を考える。

評価規準
整数を類別した際、それぞれの集合に共通する性質を見つけ、表すことができる。
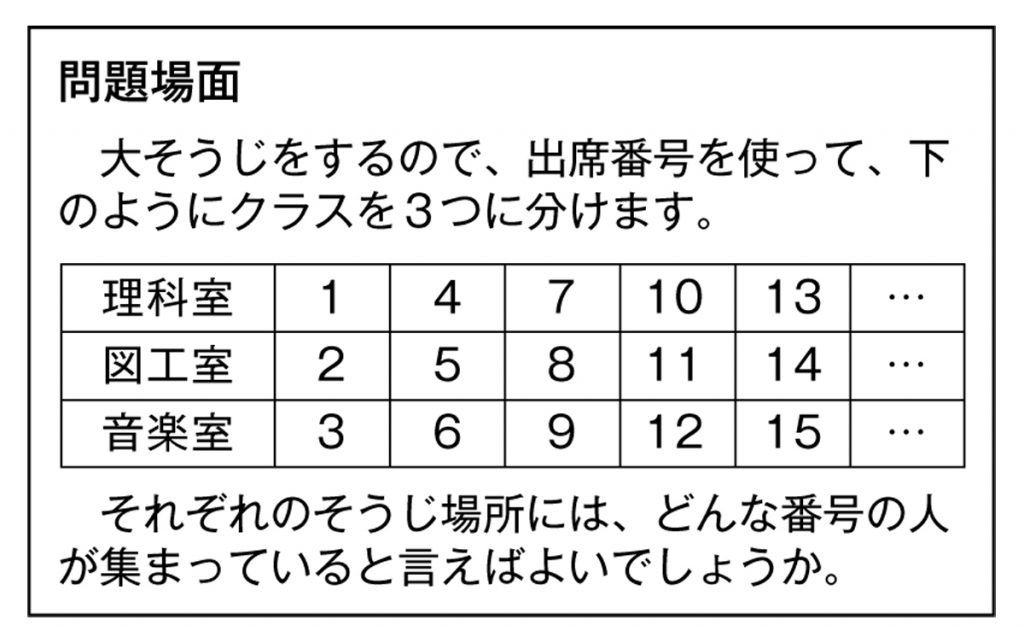
大掃除をするので、出席番号を使ってクラスを3つに分けたいと思います。どんな分け方があるかな。
もし、30人だったら理科室に1~10、図工室に11~20のように、まとめて分ければよいと思います。
1人ずつ順番に、掃除場所に分けていけばよいと思います。
なるほど。分け方にはいろいろあるけれど、この分け方は、どんな分け方をしているかな(問題提示)。
トランプを配るみたいに、分けている。
3人ずつ、順番に分けている。
なるほど。分け方については、みんなわかっているようですね。では、理科室・図工室・音楽室、それぞれの掃除担当の人たちは、どんな番号の人たちの集まりだと言うことができるでしょうか。
本時の学習のねらい
それぞれのそうじ場所のたん当者は、どんな番号の集まりと言えるか考えよう。
見通し
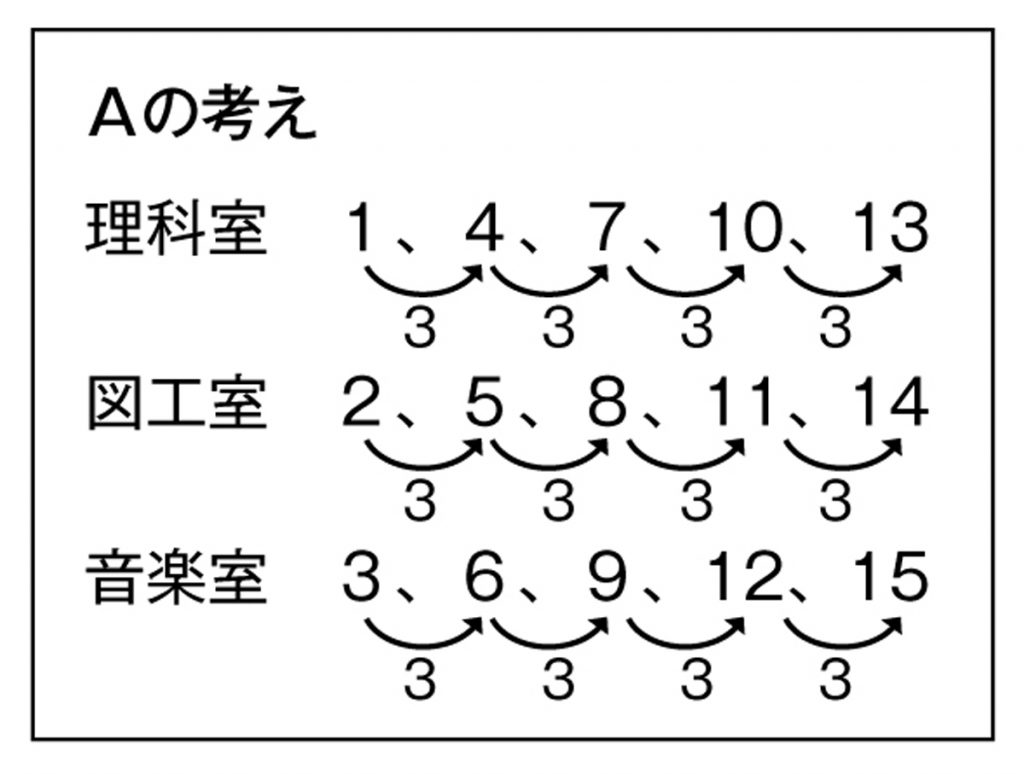
A
どの掃除場所の番号も、3ずつ増えている。
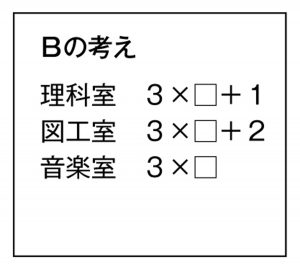
B
音楽室は、かけ算九九の3の段の答えになっている。理科室・図工室は…。
C
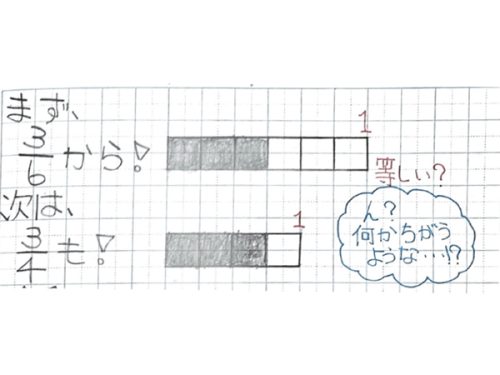
3で割ってみて、余りで考えると…。
自力解決の様子
学び合いの学習
イラスト/横井智美
『教育技術 小五小六』 2019年9月号より