小２算数「分けた大きさ」指導アイデア《分けた１つ分の大きさの表し方について考える》

特集: 文部科学省教科調査官監修｢教科指導のヒントとアイデア｣

2024.05.25

単元の展開

第１時　同じ大きさに２つに分ける（半分）という操作に着目し、分けた１つ分の大きさの表し方について、元の大きさの二分の一と言い、[MATH]\(\frac{1}{2}\)[/MATH]と書くことを知る。
▼
第２時（本時）　同じ大きさに４つ（８つ）に分けるという操作に着目して、分けた１つ分の大きさの表し方について考える。
▼
第３時　これまでの表し方に着目して、同じ大きさに３つに分けた１つ分の大きさの表し方について考える。
▼
第４時　２つの数量の関係に着目して、倍や分数の意味について捉える。
▼
第５時　チャレンジ問題や面白問題に取り組むなど、学習内容を習熟したり発展させたりする。

本時のねらい

同じ大きさに４つ（８つ）に分けるという操作を通して、分けた１つ分の大きさの表し方（[MATH]\(\frac{1}{4}\)[/MATH]、[MATH]\(\frac{1}{8}\)[/MATH]）について考える。

評価規準

同じ大きさに分けるという操作に着目し、分けた大きさの表し方を考えている。

本時の展開

今日も折り紙を使って考えていきましょう。まず、折り紙を半分に折りましょう。

それを数ではどのように表しましたか。

[MATH]\(\frac{1}{2}\)[/MATH]です。

そうでしたね。では、[MATH]\(\frac{1}{2}\)[/MATH]はどんな大きさの数でしたか。

折り紙１枚の半分の大きさです。　

折り紙を２つに折った１つ分の大きさです。　

折り紙を２つに切った１つ分の大きさです。

２つに分ければ、どんな大きさでも[MATH]\(\frac{1}{2}\)[/MATH]ですか。

同じ大きさの２つに分けた１つ分が[MATH]\(\frac{1}{2}\)[/MATH]です。

元の大きさを同じ大きさに２つに分けた１つ分、それが[MATH]\(\frac{1}{2}\)[/MATH]でしたね。では、今日はさらに紙を半分に折ってみたいと思います。

おり紙を半分におって、それをまた半分におった大きさはどれだけでしょう。

半分に折ると２つに分かれましたが、半分の半分だとどうなるのか、折り紙を広げてみましょう。どのように分かれましたか。

４つに分かれました。

付け足しです。同じ大きさに４つに分かれました。

そうですね。では、同じ大きさに４つに分けた１つ分の大きさについて考えていきましょう。

同じ大きさにいくつかに分けた１つ分の表し方を考えよう。

見通し

２つに分けた１つ分は[MATH]\(\frac{1}{2}\)[/MATH]だから、それと同じように考えればできるかな。

半分にすると[MATH]\(\frac{1}{2}\)[/MATH]になるから、半分の半分も[MATH]\(\frac{1}{2}\)[/MATH]になると思うよ。

同じ大きさの４つに分けた１つ分だから、[MATH]\(\frac{1}{4}\)[/MATH]になるんじゃないかな。

自力解決の様子

Ａ　つまずいている子
[MATH]\(\frac{◯}{◯}\)[/MATH]という考え方の理解が不十分で、「半分は[MATH]\(\frac{1}{2}\)[/MATH]」というイメージから、半分の半分も[MATH]\(\frac{1}{2}\)[/MATH]と考えている。

Ｂ　素朴に解いている子
前時の考え方を想起し、同じ大きさに２つに分けた１つ分は[MATH]\(\frac{1}{2}\)[/MATH]と表したことから、同じ大きさに４つに分けた１つ分なので[MATH]\(\frac{1}{4}\)[/MATH]と説明している。

Ｃ　ねらい通り解いている子
元の大きさを同じ大きさでいくつに分けているかに注目し、その１つ分なので、[MATH]\(\frac{1}{2}\)[/MATH]、[MATH]\(\frac{1}{4}\)[/MATH]と一般化して説明している。

学び合いの計画

学び合いの時間では、折り方の違うやり方を発表していきます。それぞれの折り方を見せ、折り方の違いで一つ一つの形は違うけれど、どれも同じ大きさの形４つに分かれていることを確認しましょう。そこから、どれも同じ大きさに４つに分けられていることから、それぞれの１つ分は「[MATH]\(\frac{1}{4}\)[/MATH]」と言えることを押さえていくようにします。

また、「半分は[MATH]\(\frac{1}{2}\)[/MATH]」ということから、半分の半分も[MATH]\(\frac{1}{2}\)[/MATH]と言えるという子供に対しては、前時のノートをふり返らせ、[MATH]\(\frac{1}{2}\)[/MATH]に分けた図を見せたり、[MATH]\(\frac{1}{2}\)[/MATH]の大きさにした折り紙を実際に見せ、本時の折り紙と比較させたりすることにより、本時の１つ分の大きさは「[MATH]\(\frac{1}{4}\)[/MATH]」と言えることをしっかり理解できるようにします。

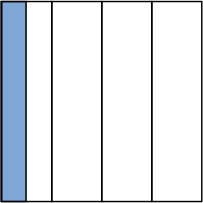
ここで、[MATH]\(\frac{1}{2}\)[/MATH]や[MATH]\(\frac{1}{4}\)[/MATH]のような数を分数ということを指導し、１、２、３という既習の数（自然数）とは大きさの違う数があることを理解させましょう。さらに、違う大きさに４つに分けた誤答例を出し、「これは[MATH]\(\frac{1}{4}\)[/MATH]ですか」と問うことで、元の大きさを同じ大きさに分けられていないものは、分数では表すことができないことを理解できるようにします。理解が難しい子供がいる場合は、[MATH]\(\frac{1}{2}\)[/MATH]のときもどうだったか、ふり返らせることも大切です。

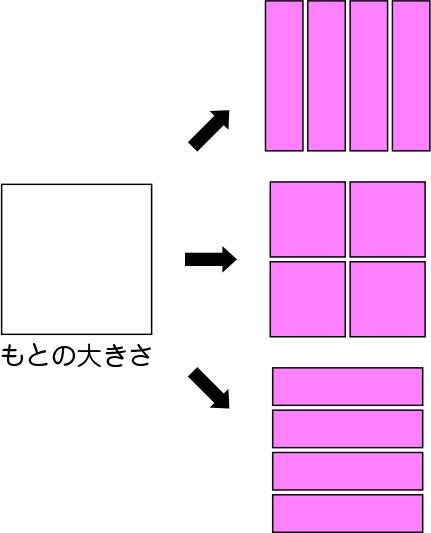
[MATH]\(\frac{1}{8}\)[/MATH]についても問題提示し、考えさせていきます。これまでと同様に、「①同じ大きさに分けられているか」「②同じ大きさにいくつに分けられているか」ということを子供と確認しながら[MATH]\(\frac{1}{8}\)[/MATH]や分数の意味の理解が深まるようにしましょう。同じ大きさに分けられているのかの確認は、子供に元の大きさの長方形を配付し、実際に折らせて確認するなど、「同じ大きさに分けられていること」をしっかりと意識させることが大切です。