小５算数「□と△を使った式」指導アイデア《伴って変わる２つの数量の関係を、□や△を使った式に表す》

特集: 文部科学省教科調査官監修｢教科指導のヒントとアイデア｣

2024.05.25

単元の展開

第１時　伴って変わる２つの数量の関係に着目し、その関係を□や△を使った式で表す。（□×３＋１＝△となる関係について）
▼
第２時（本時）これまでに学習してきた伴って変わる２つの数量の関係を、□や△を使った式に表す。（□×４＝△となる関係〈比例〉について）
▼
第３時　□や△を使った式をよみ、２つの数量の関係を表に表して考えたり、具体的な場面を考えたりする。（□＋△＝12、□－２＝△など）

●第１時のまとめ

・伴って変わる２つの数量の関係を見付けると、数が大きくなっても本数を求めることができる。

・□や△を使った式に表すと、伴って変わる２つの数量の関係が捉えやすくなる。

●第２時のまとめ

・これまでに学んできた伴って変わる２つの数量の関係も、□や△を使って式に表すと、数量の関係が分かりやすくなる。

●第３時のまとめ

・□や△を使った式をよむと、１つの同じ式でもさまざまな２つの数量の関係を考えることができる。

本時のねらい

伴って変わる２つの数量の関係を表にまとめ、表から読み取れる２つの数量の変化の仕方を基に、対応の関係を見いだし、□や△を使った式に表すことを考える。

評価規準

表から読み取れる２つの数量の変化の仕方を基に、対応の関係を見いだし、□や△を使った式に表現している。（思考・判断・表現）

本時の展開

長さの等しいぼうで、下のように正方形のだんをつくり、大きくしていきます。正方形のだんを10だんつくるとき、周りを囲むぼうは何本いりますか。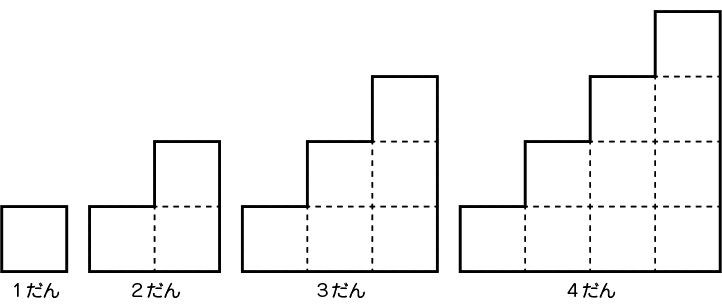

（前時のふり返り）前の時間に、長さの等しい棒で正方形を並べていき、正方形を□個つくるとき、棒は何本いるかを考えましたね。

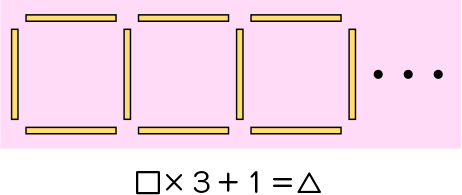
棒の数を数えなくても、２つの数の変わり方のきまりを見付けて式に表すと、数が大きくなっても本数を求められて便利だったよね。

式に表すと、伴って変わる２つの数の変化や対応の特徴が分かったよね。

それでは今日は、長さの等しい棒を使って、他の形をつくってみます。長さの等しい棒で、図のように、１段、２段、３段…･･と正方形を積んで階段の形をつくっていきます。段の周りを棒でつくります。10段つくるときの棒の数は分かりますか。

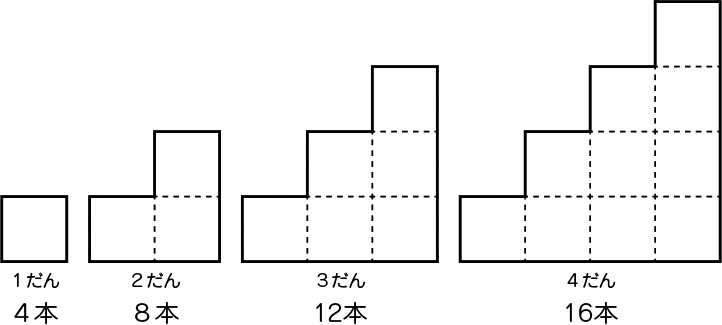
１段だったら４本。２段だったら８本。３段だったら（少し考えて）12本。

４段くらいまでだったら数えられるけれど、10段をかくのも数えるのも大変ね。

何かきまりを見付けたら、すぐに分からないかな。　

そうそう。前の時間にやったように、段の数と周りの棒の数の関係のきまりを考えるといいね。

段が増えると、周りの棒の数は増えていくけど、段の部分がでこぼこしていて分かりにくいね。

前の時間にやったように、表に表してみようかな。

それだったら、式にもできるといいよね。

２つの数の変化の様子や対応のきまりを見付ければ、式に表すことができる。そうすれば、すぐに10段のときの棒の数が求められそうだよ。

段の数を□にして、段の数につれて増えていく棒の数は△にして式を表してみよう。

それでは、伴って変わる２つの数量である段の数と棒の数の変化や対応のきまりを見付けて、□と△を使った式に表して考えていきましょう。

10段の場合を知るために、伴って変わる数量の関係を□や△を使った式に表して考えよう｡
（段の数）→　□　　（棒の数）→　△　　　　　

見通し

正方形を階段のように積んでいく図をかいて考えよう。（方法の見通し）

階段のような図のでこぼこをなおして、正方形と見て考えよう。（方法の見通し）

段の数と棒の数の関係を表に表して、２つの数の関係を考えよう。（方法の見通し）

□（段の数）と△（棒の数）として、□と△の関係を式に表そう。（結果の見通し）

２つの数の関係を式に表して、どんな数でも分かるようにしよう。（結果の見通し）

自力解決の様子

A　つまずいている子
□が10段のときは４×10で40本　
・階段状の図をかいて、１本ずつ数えて、40本を求めている。
・数えて求めた40本をよりどころに、40本と10段から、式を立てようとしている。
　　↓
10段の場合を求めるだけで考えが止まっている。

Ｂ　素朴に解いている子
式は10×４で、□が10段のときは40本　
・一辺の長さが10の正方形をかいて、10×４＝40と求めている。
　　↓
「正方形の周りの長さは一辺の４倍」ということから「棒の数は段の数の４倍」ということにつなげて考え、□や△を使った式に表そうとしている。

Ｃ　ねらい通り解いている子
式に表すと、□×４＝△
表をつくって、

・どの数でも、□の４倍が△になっている。
・式は、□×４=△
・□×４=△だから、□が10のとき、△は40
・段の数が10のとき、10×４で棒の数は40本
　　↓
□と△は比例していること、比例の関係も□と△で表すことができることに着目している。

学び合いの計画

本単元では、伴って変わる２つの数量を、□や△を使った式に表すことのよさを感じることが大切です。そして、本時（２／３時）では、既習事項である「比例」の関係も□や△を使った式に表すことができるのかを考えていきます。この学習は、第６学年の「文字式」の学習や中学校の関数の学習にもつながる大切な単元です。

まず、子供たちが「難しそうだけれどやってみたい。いい方法を見付けたい」と主体的に取り組むことができるように、子供たちの実態に合った問題の提示が大切です。第１時から少し発展した問題に手応えを感じながら、問題に取り組んでいくでしょう。そして、問題解決の場では、自分で解決する方法を選択しながら学習を進めることができる学習の積み重ねが大切です。分からないときには、友達や教師に聞いたり、教科書やインターネットで調べたりする自己解決の方法も学んでおくとよいでしょう。

本時では、特に２つの数の変化や対応の様子を図や表で表すことがポイントになります。図や表から伴って変わる２つの数量の変化の特徴を見付け、それを式や言葉で表すことで、既習事項である比例の関係にあることに気付くでしょう。比例も□や△の式で表せるのかなと考えを深めていきましょう。

１人１台端末活用ポイント

一人一人が考えたことを画面共有することができると、一人一人の発表の時間を取らずに、子供たちどうしが友達の意見を基にして考えを加えたり見直したりすることができます。つまずいている子供にとってはヒントになり、安心して学習を進めることができるでしょう。また、教師としても、子供たちの考えを基にアドバイスをしたり、子供たちの考えの傾向を理解したりしやすくなります。

本単元では、伴って変わる２つの数を表した表や、変化の様子を表した図、そして、自分なりに考えた□と△を使った式を共有することがポイントになり、子供たちが関わって学び合うきっかけになります。□の値だけを入れてある表や、１段、２段、３段くらいまでの図を準備しておくと、子供たちはどんどん次の数を知りたくなり、わくわくしながら考えたくなるきっかけになるでしょう。