小6算数「場合の数」指導アイデア《重複がある並びの整理の仕方》

執筆/福岡教育大学附属久留米小学校教諭・藤木宏平
監修/文部科学省教科調査官・笠井健一、福岡教育大学教授・清水紀宏

目次
単元の展開
第1時 重複のないすべての並びを図や表に表し、起こり得る場合の意味を捉える。
▼
第2時 起こり得る場合を図や表などに表し、重複なしで選ぶ並びについて落ちや重なりがない整理の仕方を捉える。
▼
第3時(本時)起こり得る場合を図や表などに表し、重複ありの並びについて落ちや重なりがない整理の仕方を捉える。
▼
第4・5時 起こり得る場合を図や表などに表し、重複なしの組み合わせについて落ちや重なりがない整理の仕方を捉える。
▼
第5時 起こり得る場合を図や表などに表し、逆の組み合わせを用いる場合について落ちや重なりがない整理の仕方を捉える。
▼
第6時 さまざまな起こり得る場合を図や表などに表させ、落ちや重なりがない整理の仕方を捉える。
本時のねらい
事象の特徴(重複がある場合に並べる)に着目し、落ちや重なりなく並べる方法を考えることができる。
評価規準
重複がある場合の問題について、樹形図を用いて、落ちや重なりなく並べることができる。(思考・判断・表現)
本時の展開

3回㋐か㋑を選んで、文字の並びを当てる宝くじがあります。同じ文字を選んでもよいです。絶対に当てるために、何枚のカードがいるでしょう。
【前時問題場面】
小説(シ)、伝記(デ)、サイエンス(サ)、歴史(レ)の本から3冊を選んで本棚に並べます。どんな並びがありますか。
※前時問題場面と本時問題場面を提示した後
前回の場面と違うところは何ですか。
本から宝くじに場面が変わっています。
前回は、同じ本は選べませんでした。今回は、同じ文字を選ぶことができます。
今、太郎さんはこのように塗って㋐㋐㋑になりました。これで絶対当たると言えますか。
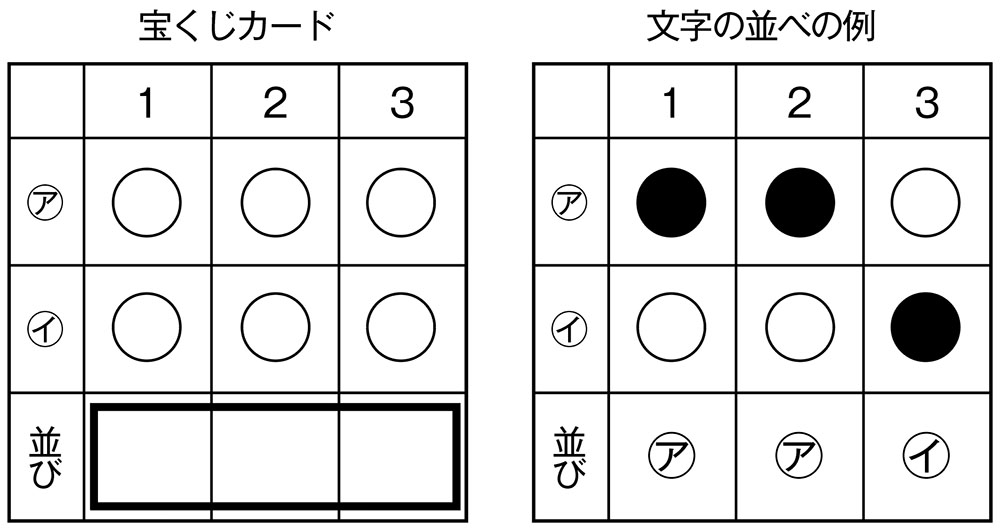
言えないと思います。当たりは、㋐㋑㋐かもしれません。
そうですね。もし、宝くじをたくさん買えるとして、絶対に当てるためにはどうするといいですか。100枚ぐらい買えば絶対当たりますか。
100枚も買わなくてよいと思います。
100枚買うと当たるかもしれないけど、効率が悪いと思います。
すべての並び方のくじを買えばよいと思います。分かれば、絶対当てることができます。
すべての並びが何通りか調べると、買う枚数が分かります。
確かに、すべての並びが何通りか分かると、何枚買えばよいか分かりますね。
同じものも使えるから多くなりそう。
では今日は、どのようなめあてにしますか。

同じものを並べてもよいときの、落ちや重なりのない並べ方を考えよう。
見通し
- 方法→最初を固定、樹形図、表
- 結果→10枚以上
自力解決の様子
A つまずいている子
観点を決めることができず、落ちや重なりがある。

B 素朴に解いている子
観点を決めて、表に整理して起こり得るすべての場合をかいている。

答え 8枚
C ねらい通り解いている子
観点を決めて、樹形図に整理して起こり得る場合をかいている。
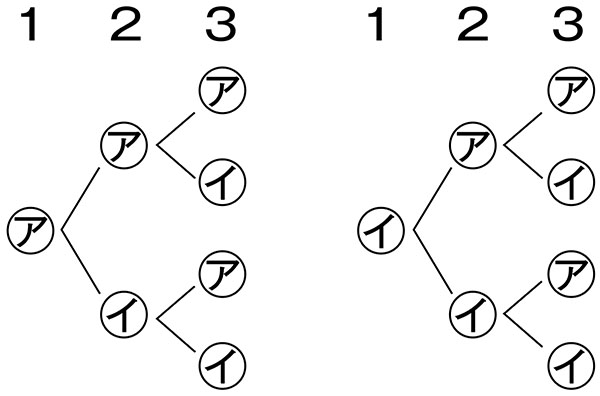
答え 8枚
学び合いの計画
自力解決の段階で、1人1台端末を活用して、自他の解決方法を共有できるようにし、互いの解決方法を見合うことができるようにしておきます。
イラスト/横井智美

