３年生「分数」「筆算（×２けたのかけ算）」【「算数つまずき防止」ここがポイント！#４】

2022.12.02

間違った子供の側に教師が立ってみるのもよい

３年生で子供たちが最もつまずきやすいのは、「分数」だと思います。

子供たちは２年生のときにも分数の学習をしていますが、そのときには、例えばピザを２等分とか４等分にして、「こちらが[MATH]\(\frac{1}{2}\)[/MATH]だよ」「こっちは[MATH]\(\frac{1}{4}\)[/MATH]と言うんだよ」というような学習をしています。いわゆる、分割操作を表す際に使われる数としての学習が主です。

それが３年生になると、量を表す際に使われる数としての分数の学習に入っていきます。それによって例えば、[MATH]\(\frac{1}{3}\)[/MATH]mとか[MATH]\(\frac{1}{4}\)[/MATH]mというように、量を表す分数の学習に入り、分数が使われる範囲が広がってきます。そこで困る子が出てくるのです。

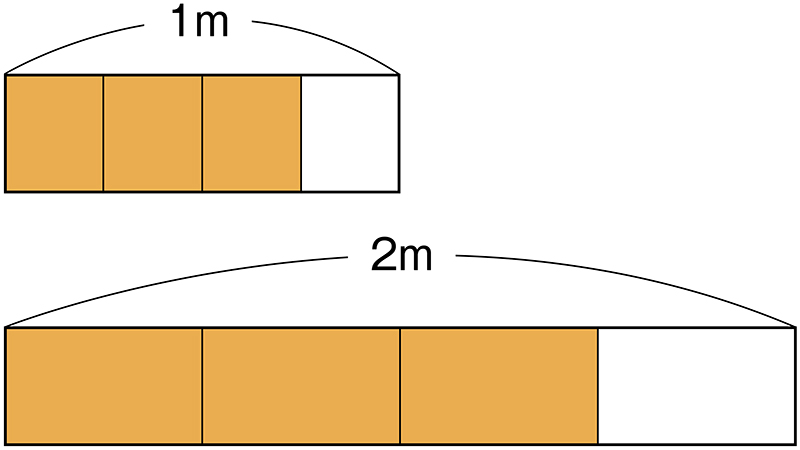
よくある例を挙げてみましょう。例えば、１mの長さを４等分している図があり、もう一方に２mを４等分している図があるとします（資料参照）。どちらの図でも、全体の[MATH]\(\frac{3}{4}\)[/MATH]のところを指し示しており、「それぞれ何メートルですか？」と問うと、「どちらも[MATH]\(\frac{3}{4}\)[/MATH]mです」と答えたりします。実際に授業をしてみると、こういうつまずきが結構多く見られることに気付くはずです。分割操作を表していた、２年生の分数の考え方から離れられていないわけですね。ここで大事なのは、基になる量が何かということなのですが、そういう視点で捉えることが難しいわけです。

では、どのような指導をしていけばよいのかということになりますが、まず事前に具体物を使いながら実感を伴う学習をすることが大切だと思います。

例えば、「１mを３等分します。分けた１こ分の長さは何mと言えばよいでしょうか？」という問題があるとします。そのときに、１mを３等分したものの１こ分（[MATH]\(\frac{1}{3}\)[/MATH]m）を、実際に紙テープのような具体物を使って作ってみるのです。それは[MATH]\(\frac{1}{3}\)[/MATH]mだけでなく、３等分したものの２こ分（[MATH]\(\frac{2}{3}\)[/MATH]m）だったり、４等分したものの３こ分（[MATH]\(\frac{3}{4}\)[/MATH]m）だったりと、いろいろと紙テープを使って作っていくわけです。そうした学習を通し、基になるものを等分することや量感を育むことなどが後々の学習に生きてきます。

もちろん、事前にそのような学習をしていても、１mの[MATH]\(\frac{3}{4}\)[/MATH]と、２mの[MATH]\(\frac{3}{4}\)[/MATH]とを問う問題で、「どちらも[MATH]\(\frac{3}{4}\)[/MATH]メートルです」と答える子供は必ず出てくるでしょう。そのときにはまず、「どうして、[MATH]\(\frac{3}{4}\)[/MATH]メートルだと思ったの？」と尋ね、そう考えた理由を聞きたいところです。そこで子供の間違った考えを聞いても、教師がその場で訂正したり反証したりするのではなく、「確かに、どっちも４等分したものの３つだものね」と、間違った子供たちの側に立ってみるのもよい方法だと思います。

そうすると、必ず反対意見の子供たちの中から、「こっちは基の長さ１mを４等分していて、こっちは２mを４等分しているじゃない」と、基の長さに着目した意見が出てくるはずです。それを価値付けて、「ああ、そうだよね！　前に勉強したね」と評価していくのです。そうした子供たちの意見を聞いて、間違っていた子供たちからも「あっ、そうか」という声が聞こえてくるでしょう。そのように、教師の大人目線の論理的な説明ではなく、ほかの子供たちの言葉で納得できるようにしていくのが、どの子供にとっても理解を深めるうえで効果的だと思います。その学習過程で、子供たちから事前の学習をふまえて、「前、[MATH]\(\frac{3}{4}\)[/MATH]mを作ったとき、１mよりも短かったよ」というように、体験に基づいた発言ができればよいなと思います。

さらに、学習を深めていくためには、式だけでなく数直線やテープ図、（さらにほかの単元では）表やグラフなども併記しながら、言葉と式や図、表やグラフなどを行き来しながら学習していくことが大切です。