小3算数「かけ算の筆算」指導アイデア(11/11時)《答えが一番大きくなるかけ算をつくりましょう》
執筆/富山県公立小学校教諭・本間大輔
編集委員/文部科学省教科調査官・笠井健一、前・富山県公立小学校校長・中川愼一
目次
本時のねらい(本時11/11時 内容を一通り学習した後の活用の時間)
かけ算の筆算の位ごとに分けて計算するしくみとその意味について考える。
評価規準
かけ算の筆算のしかたをふり返り、位ごとのかけ算の大きさを考えながら、計算に関して成り立つ性質(分配法則)をうまく活用している。(思考・判断・表現)
問題
□の中に1から4までの数を一つずつ入れて、答えが一番大きくなるかけ算をつくりましょう。
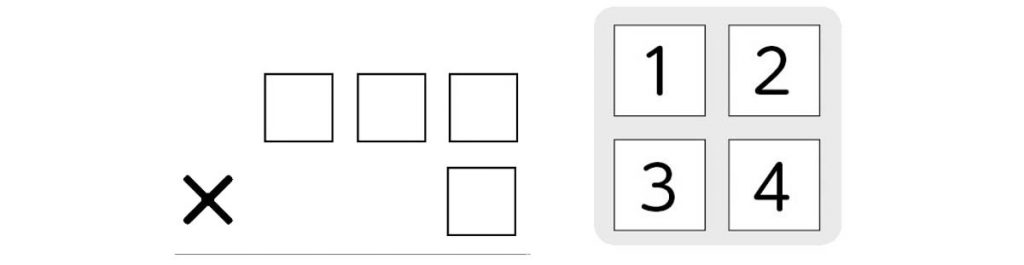
答えが一番大きくなるようにするには、どこにどの数を入れたらよいですか。
一番大きい4を百の位に入れます。一番小さい1は一の位に入れます。
百の位の数が大きいと答えも大きくなりそうだね。
かけ算だから、大きい数どうしをかけたら、答えは大きくなるはずだよ。
かけ算の筆算は位ごとに計算するから、そのことをうまく使えばできそうだよ。
学習のねらい
かけ算の筆算のしくみをうまく使って考えよう。
見通し
・かけ算の筆算のしくみ(位ごとに計算した結果を足して答えを出す)を使って考えたらよさそうだ。 [方法の見通し]
・百の位とかける数に大きい数を入れたらよさそうだ。[方法の見通し]
・「4□□×3」か「3□□×4」が最も大きな答えになりそうだ。[結果の見通し]
自力解決の様子
A つまずいている子
小さい数から順に入れたり、無作為に入れたりして試している。
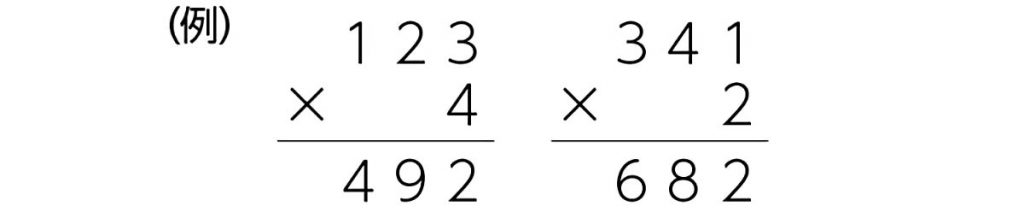
B 素朴に解いている子
大きい数から順に入れて、考えている。
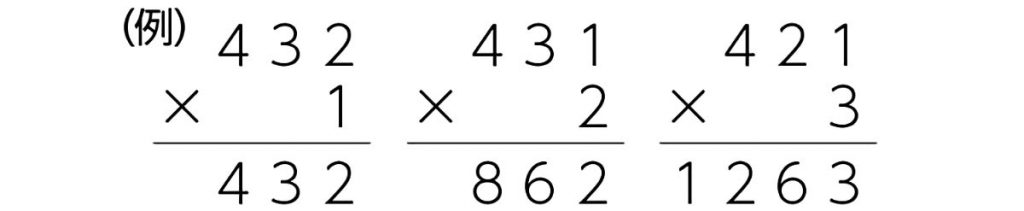
C ねらい通り解いている子
「421 ×3」と「321 ×4」に絞り込んで考えている。
「321 ×4」が大きいわけを筆算の手続きと意味に基づいて、式や図を用いて考えている。
学び合いの計画
全体発表の場では、一番小さい数の「1」がかけられる数の一の位に、二番目に小さい数の「2」が十の位に入るところまでみんなで考えを進めて、考える対象を絞り込みます。
イラスト/小沢ヨマ、横井智美
『教育技術 小三小四』2021年10/11月号より