小4算数「かんたんな割合」指導アイデア
執筆／福岡教育大学附属久留米小学校教諭・廣木伸幸
編集委員／文部科学省教科調査官・笠井健一、福岡教育大学教授・清水紀宏
目次
本時のねらい（本時1／3時 単元導入）
倍の関係に着目し、2つの数量どうしの比較では、差だけでなく、割合を使って比較することができることを理解する。
評価規準
2つの数量の割合を使って、2つの数量の関係の比べ方を考え、説明することができる。（思考・判断・表現）
問題1
下の表のようなゴムがあります。どちらのゴムのほうがよくのびると言えますか。
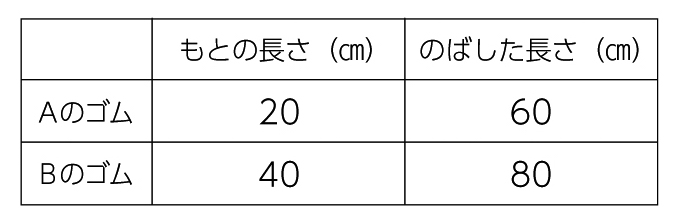
手作りマスクを作るためにゴムひもを使います。よく伸びるゴムを使いたいです（問題と実際のゴムひもを提示）。どちらのゴムがよく伸びると言えますか。
元の長さと伸ばした長さの差が同じだから同じだと思います。
（実際に伸ばしてみて） Aのほうが伸びる気がする。
「長さの差」のほかに比べ方があるのかな。
では、今日は2つの量の関係の比べ方を調べましょう。
学習のねらい
2つの量の関係の比べ方を調べよう。
見通し
- 「元の長さ」と「伸ばした長さ」の関係。〔着目の見通し〕
- テープ図に表す。〔方法の見通し〕
- 同じ。〔結果の見通し〕
- Aのほうがよく伸びる。〔結果の見通し〕
自力解決の様子
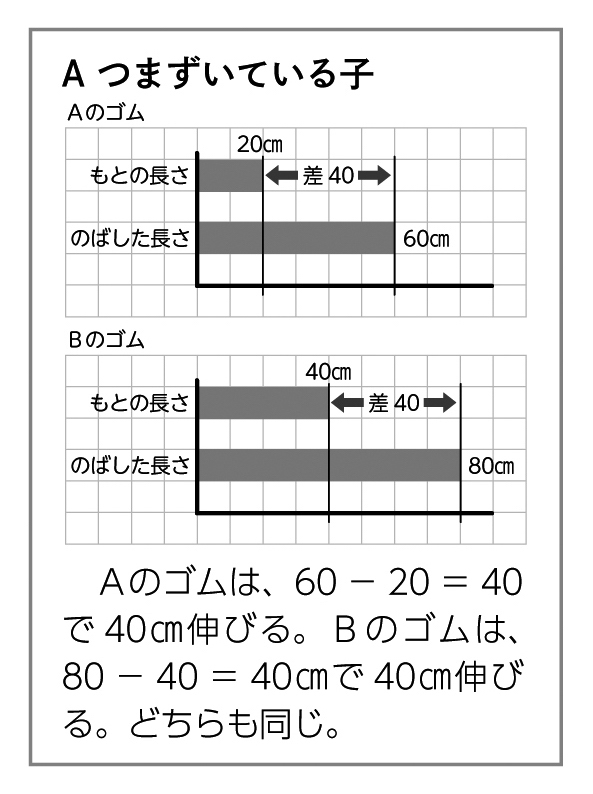
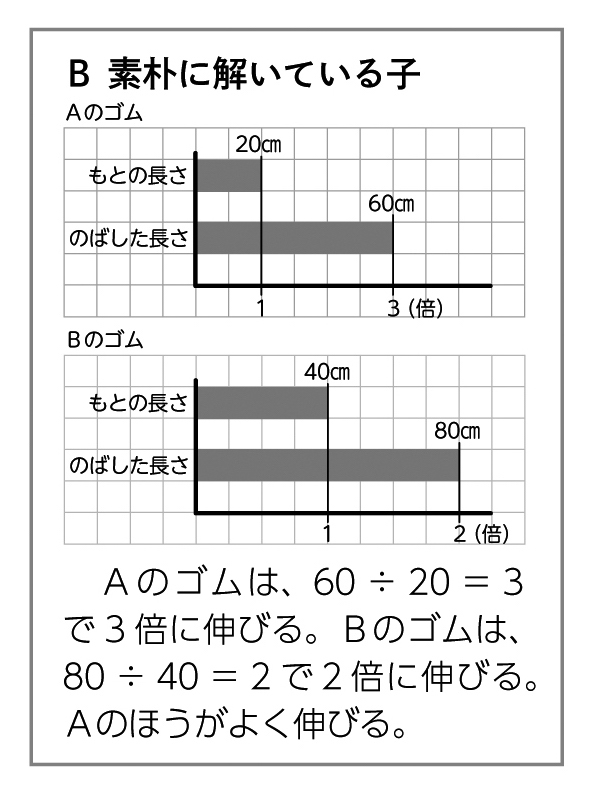
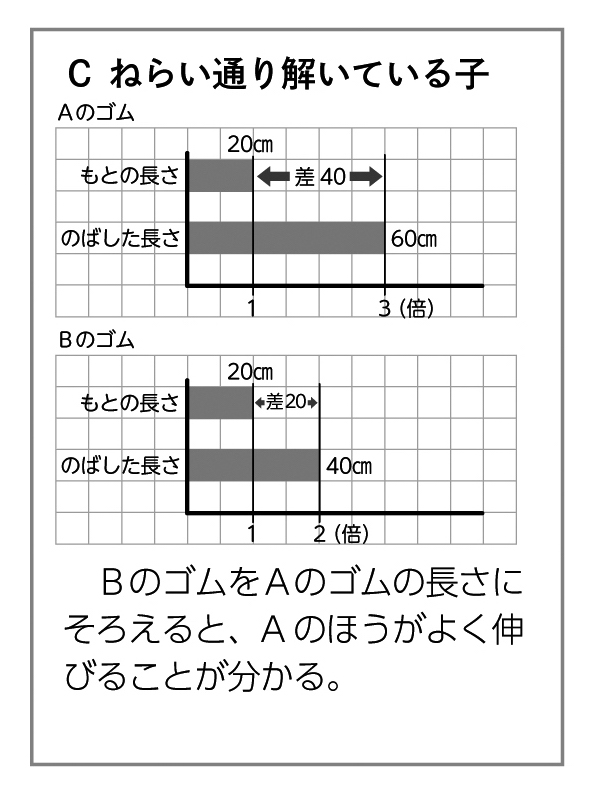
学び合いの計画
イラスト／横井智美
『教育技術 小三小四』2021年8/9月号より
