小4算数「資料整理」指導アイデア《二つの分類項目をもつデータの分類整理》

特集: 【文部科学省教科調査官監修】1人1台端末時代の｢教科指導のヒントとアイデア｣

2022.08.15

単元の展開

第１・２時　データを二つの観点から分類整理する方法や二次元表の表し方、特徴の調べ方について考え、理解を深める。
▼
第３時（本時）二つの分類項目をもつデータを、二つの観点から分類整理し、二次元表に表すことについて考える。

１人１台端末活用ポイント

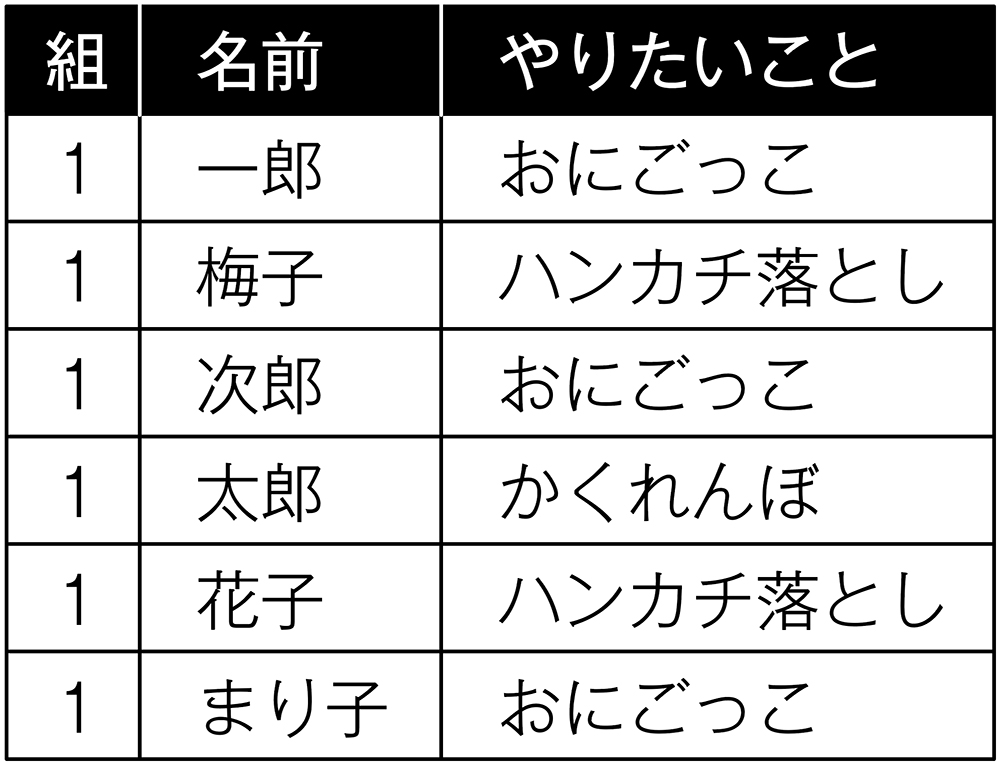
４年１組35人と４年２組34人で遠足に行きます。遠足では自由活動の時間があり、どのようなグループで、どのような活動をするか自分たちで相談して決めることになっています。そこで、どのような遊びをしたいかアンケートをとることにしました。アンケート結果から、グループや活動を決めるには、どうしたらよいでしょうか。

アンケート結果のデータを端末にアップし、一覧を共有して活用できるようにします。
また、アンケートの答えを入力できるようなスプレッドシートを端末にアップしておくことで、実際のデータを基に考えることができ、データを二次元表に表す目的意識を高めることができます。

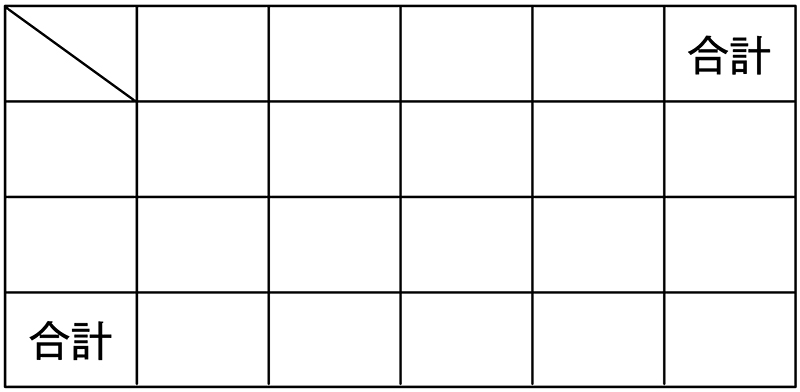
次に、遠足のお弁当に入れてほしいおかずは、たまご焼きとハンバーグのどちらがよいか、アンケートをとりました。その結果、たまご焼きを選んだ人は41人、ハンバーグを選んだ人は28人、１組でたまご焼きを選んだ人は22人でした。２組でハンバーグを選んだ人は、何人でしょう。

書き込み可能な二次元表を数種類（項目の数を選べるように）端末にアップしておくことで、１組２組と活動や、男女と活動などで整理できるようにします。
また、端末を活用することで、作成した二次元表から特徴を考える際、数種類の二次元表を比較しやすくなります。

本時のねらい

（二つの観点から分類整理する学習の後）
二次元表の意味に照らし合わせながら、ピーマンも玉ねぎも好きな子供の人数について、分かっている数字を手がかりに筋道を立てて求めていく方法について考える。

評価規準

二つの分類項目をもつデータを、二つの観点から落ちや重なりがないように分類整理する方法を考えたり、二次元表と対応させて考えたりするなど、問題に対する結論を考えている。（思考･判断･表現）

本時の展開

遠足の行きのバスで、４年１組では、好きな野菜の話になりました。４年１組35人中、ピーマンが好きな人は24人、玉ねぎが好きな人は20人、両方きらいな人は４人でした。両方好きな人は、何人でしょう。

遠足の続きの問題ですね。ピーマンも玉ねぎも両方好きな人は、何人いるでしょうか。

ピーマンが好きな人は24人で、玉ねぎが好きな人は20人だから、24＋20で44人です。

えっ？　でも、４年１組は、35人しかいないよ。44人だと、35人を超えてしまっているよ。

確かにそうだね。ピーマンが好きな24人のなかには、「ピーマンも玉ねぎも好き」と「ピーマンは好きだけど玉ねぎは嫌い」が合わさっているのかな。

じゃあ、両方嫌いな人は４人だから、35−４で31人はどうかな。

ピーマンが好きな人が24人しかいないのに、両方好きな人がそれより多い31人になることはないのではないかな。

う〜ん、文章のままでは分かりにくいなあ。

これまで勉強してきた２つのことを合わせた表に表したら、分かりやすくなるのではないかな。

そうですね。今分かっていることを表に表してみましょう。今日使う表は、このような表ですよ。

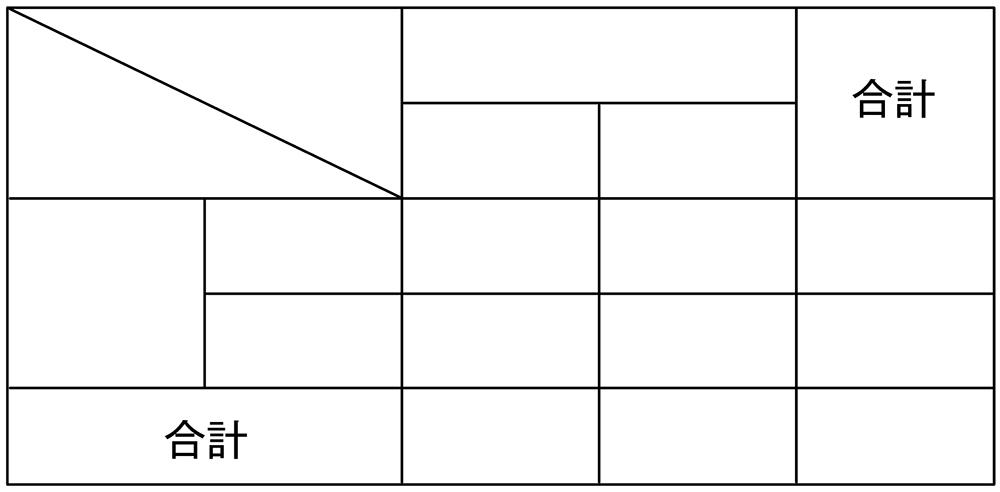
昨日までの表と違うよ。一つの項目がさらに二つに分かれているよ。

好きと嫌いの二通りがあるからかな。

ピーマンも玉ねぎも好きな人の数の求め方を考えよう。

見通し

・考えられるパターンが、全部で何パターンあるのか書き出そう。（方法の見通し）
　→　ピーマン、玉ねぎの両方が好き　　　（A）　
　　　ピーマンは好きだが、玉ねぎは嫌い　（B）　
　　　ピーマンは嫌いだが、玉ねぎは好き　（C）　
　　　ピーマン、タマネギの両方が嫌い　　（D）　
・分かっている人数を表に書き込み、何が分からないのかはっきりさせよう。（方法の見通し）
・ひき算を使えば、分からない部分も分かりそう。（結果の見通し）

自力解決の様子

A つまずいている子

・両方好きな人数は44人
分かっている数字を、表のどこに当てはめていいか分からない。

Ｂ素朴に解いている子

・両方好きな人数は13人
分かっている数字を表に当てはめたり、表の残りの部分に入る数字を計算で求めたりしている。

Ｃねらい通り解いている子

両方好きな人数は13人
・表の横と縦の項目に着目して、四つの場合が表のどこに当てはまるかを考えている。一つの観点から見た場合の数が、表のどこに当てはまるかを考えている。

学び合いの計画

二次元表の意味を考えながら、分かっている数字を手がかりに、筋道を立てて考えていくことが大切です。そこで、まずは問題場面から、分かることと分からないことを整理します。そして、どのような場合があるのかを考えていきます。

その際、「ピーマンは好きだが、玉ねぎは嫌い」のように、言葉で表現することを大切にしていきます。次に、起こり得る場合が、表のどこに当てはまるのかを考えたり、その理由を話し合ったりしましょう。

さらに、一つの観点から見た場合の数が、表のどこに当てはまるかを考えたり、その理由を説明したりしましょう。例えば、問題場面から分かる「玉ねぎが好きな人は20人（①）」とは、先に考えた起こり得る場合の「ピーマン、玉ねぎの両方が好き（Ａ）」と「ピーマンは嫌いだが、玉ねぎは好き（Ｃ）」の両方であることから、表の合計①の部分に当てはまると説明できるようになることが大切です。

ノート例

全体発表とそれぞれの考えの関連付け

ピーマンも玉ねぎも好きな人の数は分かりましたか。

ピーマンも玉ねぎも両方好きな人は13人です。A＋11＝24だから、24－11をして求めました。

私も両方好きな人は13人になりました。でも、式は20－７になりました。どうしてかと言うと、A＋７＝20だからです。

24はピーマンが好きな人数、20は玉ねぎが好きな人数なのは分かるけど、11や７はどこから出てきたの。

11と７も、ひき算をして求めることができるよ。11は、35－24をして……。

ちょっと待って。式だけ聞いていても、一体何のためにその計算をしているのか分からないよ。

では、表とつなげながら考えていきましょう。

問題場面には、「ピーマンが好きな人」「玉ねぎが好きな人」「両方嫌いな人」しか書かれていないけど、もっと細かく分けられるよ。

そうそう。「ピーマン、玉ねぎの両方が好きな人」「ピーマンは好きだが、玉ねぎは嫌いな人」「ピーマンは嫌いだが、玉ねぎは好きな人」「ピーマン、タマネギの両方が嫌いな人」の四つのパターンに分けられるよ。

表の縦と横に注目して見ると、「ピーマン、玉ねぎの両方が好きな人」は表のＡ、「ピーマンは好きだが、玉ねぎは嫌いな人」は表のＢ、「ピーマンは嫌いだが、玉ねぎは好きな人」は表のＣ、「ピーマン、タマネギの両方が嫌いな人」は、表のＤに当てはまるね。

だから、表のＤには、４が入ることが分かるよ。

そして、今知りたいのは、ピーマンも玉ねぎも好きな人だから、表のＡに入る数が分かればいいんだね。

でも、このままではまだ分からないよ。

次は、問題場面から分かっている「ピーマンが好きな人は24人」が、表のどこに当てはまるか考えていけばいいよ。

玉ねぎが好きか嫌いかは関係なくて、ピーマンのことだけを言っているから、表の横にだけ注目して見るといいね。だから、表の③に当てはまるよ。

つまり、「ピーマンが好きな人」は、「Ａピーマン、玉ねぎの両方が好きな人」と「Ｂピーマンは好きだが、玉ねぎは嫌いな人」の合計になるのね。

同じように考えると、問題場面から分かる「玉ねぎが好きな人は20人」は、表の縦にだけ注目して見るといいから、①に当てはまるんだね。

アは、４年１組の人数35人が入るよ。

これで、もう両方好きな人数が分かりましたか。

まだ分かりません。でも、次は、表の②と④が求められそうです。②は、20＋②＝35になるから、35－20をして、15になります。

その式は、何を表しているのですか。

玉ねぎが好きな20人と玉ねぎが嫌いな②の人を合わせたら35人になるという意味です。だから、35人中玉ねぎが好きなのは20人だから、残りの15人は玉ねぎが嫌いだということを表しています。

そうそう。④は、ピーマンが好きな24人とピーマンが嫌いな④の人を合わせたら35になります。式にすると、24＋④＝35です。だから、35－24をして、11ということが分かります。

次は、表のＢとＣを求めることができそうだよ。表のＢは、「ピーマンは好きだが、玉ねぎは嫌いな人」だったね。玉ねぎが嫌いな15人は、ピーマンが好きな人Ｂ人とピーマンが嫌いな人４人を合わせた人数だから、Ｂ＋4＝15の式になるよ。

だから、15－４をして、11ということが分かるのだね。

同じように考えると、表のＣは、「ピーマンは嫌いだが、玉ねぎは好きな人」だから、ピーマンが嫌いな人11人は、玉ねぎが好きなＣ人と玉ねぎが嫌いな４人を合わせた人数。Ｃ＋４＝11の式になるから、11－４をして７になるね。

あっ！　分かった。表のＡ「ピーマン、玉ねぎの両方が好きな人」を求めるのに、24－11と20－７の２種類の式が立てられる！

24－11の式は、表の横に注目して、ピーマンが好きな人の合計から求めているね。

ピーマンが好きな人24人は、玉ねぎが好きなＡ人と玉ねぎが嫌いな11人を合わせた人数。Ａ＋11＝24の式になるから、24－11をして13になるね。

20－７の式は、表の縦に注目して、玉ねぎが好きな人の合計から求めているのだね。

玉ねぎが好きな20人は、ピーマンが好きなＡ人とピーマンが嫌いな人７人を合わせた人数。Ａ＋７＝20の式になるから、20－７をして13になるね。

どちらで考えても、ピーマンも玉ねぎも両方好きな人数が13人だと求められるね。

表に表すと分かりやすくなるね。

表の縦と横に注目して、考えられるパターンを全部出すことや、表を縦や横に注目して見たりすることが大切なのね。

表の縦と横に注目
Ａ：ピーマン、玉ねぎの両方が好きな人　　　　　　　
Ｂ：ピーマンは好きだが、玉ねぎは嫌いな人
Ｃ：ピーマンは嫌いだが、玉ねぎは好きな人
Ｄ：ピーマン、タマネギの両方が嫌いな人
表の横に注目
③：ピーマンが好きな人（Ａ＋Ｂ）
④：ピーマンが嫌いな人（Ｃ＋Ｄ）
表の縦に注目
①：玉ねぎが好きな人（Ａ＋Ｃ）
②：玉ねぎが嫌いな人（Ｂ＋Ｄ）

・起こりうる場合のすべてを分類することが大切。
・起こりうる場合を表に表すと分かりやすい。

評価問題

下のような表に表したほうがよいものは、次のうちどれですか。

① 富山市の１年間の気温の変わり方のようす
② ４年生が先週、図書室で借りた本の数
③ 犬やねこをかっている人とかっていない人
④ どの学年が、どんなけがを多くするか

子供に期待する解答の具体例

③ 犬やねこを飼っている人と飼っていない人

本時の評価規準を達成した子供の具体の姿

提示した二次元表が、二つの分類項目をもつデータを整理するのに適していることに気付いている。
二つの分類項目をもつデータを判断している。

感想例

問題場面を表に表すと、分かりやすくなりました。頭のなかも整理できた感じです。
アンケート結果をまとめるときは、考えられるすべての場合がひと目で分かるような表をつくりたいです。
そのためには、考えられる場合を全部書き出したり、それぞれの項目と表をつなげて見たりすることが大切だと分かりました。

イラスト／横井智美

小学館IDをお持ちの方はこちら

初めてご利用の方