小２算数「分数」指導アイデア（1/7時）《同じ大きさに分けているのはどれ》
執筆/福岡県公立小学校教諭・早川幸次郎
編集委員/文部科学省教科調査官・笠井健一、福岡教育大学教授・清水紀宏
目次
本時のねらいと評価規準
[本時1/7:導入]
ねらい
「[MATH]\(\frac{1}{2}\)[/MATH]」の意味を理解する。
評価規準
いろいろな分け方について、もとの大きさの[MATH]\(\frac{1}{2}\)[/MATH]であることを理解している。[知識・理解]
問題場面
サンドイッチをいろいろな形に2つに切りました。同じ大きさに分けているのはどれでしょう。
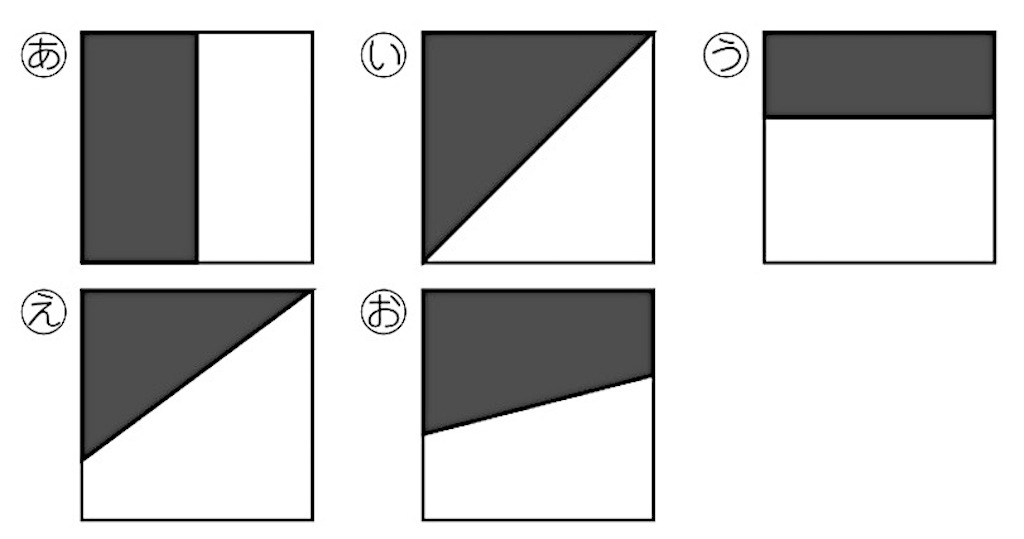
同じ大きさとは、どういうことですか。
ちょうど半分のこと。
真ん中で分けていること。
(
~
の正方形の紙を配付する。)
同じ大きさかどうかを、どのようにして調べますか。
2つに切って、ぴったり重ねて調べます。
折り曲げて、重なるかどうか調べます。
正方形のサンドイッチを切り分けるという問題場面を設定します。同じ大きさとはどういうことか問いかけ、切った2つの形の大きさが同じで、もとの大きさの半分ずつであることを確認しておきます。このことを具体物を用いた活動を通して実感するのが本時の主眼となります。
そのために、~
の分け方が描かれた正方形の紙を配付します。子どもたちとのやりとりを通して、切り分けた2つの形を重ねる方法や折り曲げて重ねる方法を見通していきます。
本時の学習のねらい
切ったり折ったりして、同じ大きさになっているか調べよう。
自力解決の様子
A つまずいている子
どこを切ったり、折ったりしたらよいか分からない、あるいは、切ったり折ったりするだけで、同じ大きさの判断ができていない。
B 素朴に解いている子
切る方法、または折る方法のどちらかで、
について、同じ大きさに分けていることを判断できている。
C ねらい通りに解いている子についても、切って重ね合わせることで、半分の大きさになっていることに気付いている。
Aの子どもには、正方形の色のついた部分とついていない部分、その2つがぴったり重なり合うと同じ大きさと言えることを確認し、線で折ったり曲げたりするよう促しましょう。
また、操作だけで終わっている子どもには、を例として、「同じ大きさに分けている」ことの意味を理解させ、や
について調べさせましょう。
Bの子どもには、について、切って動かしてみて、重なるかどうか調べるよう促しましょう。Cの子どもには、特にが同じ大きさに分けられていることを調べる時に、折るだけでは分からないことなどの気付きをノートに書くよう促しましょう。
自力解決を踏まえた全体交流
は、縦や斜めに折ってぴったり重なり合うこと、
は、重ね合わせても大きさが異なること、は、折るとぴったり重なり合わないが、切って回転させるとぴったり重なり合うことを、子どもに発表させます。机間巡視で子どもの様子を観察し、とであれば発表できる子ども、も発表できそうな子どもを把握しておき、一人でも多くの子どもが発表できるように配慮しましょう。全体交流の場面では、実際に具体物を操作しながら提示し確認させることを大切にしましょう。その後「[MATH]\(\frac{1}{2}\)[/MATH]」の意味や、 読み方、書き方を指導します。
イラスト／コダシマアコ、横井智美
『教育技術 小一小二 』2020年2月号より
