小5算数「単位量あたりの大きさ」指導アイデア
執筆/東京都公立小学校教諭・大村英視
編集委員/文部科学省教科調査官・笠井健一、東京都公立小学校校長・長谷豊
目次
本時のねらいと評価規準
本時の位置 1/4
ねらい
にわとり小屋の面積とにわとりの数が異なる場合の込み具合の比べ方を考える。

評価規準
にわとり小屋の面積とにわとりの数が異なる場合、一方の数をそろえて、もう一方の数で比べたり、単位量あたりの大きさで比べたりする方法を考えている。
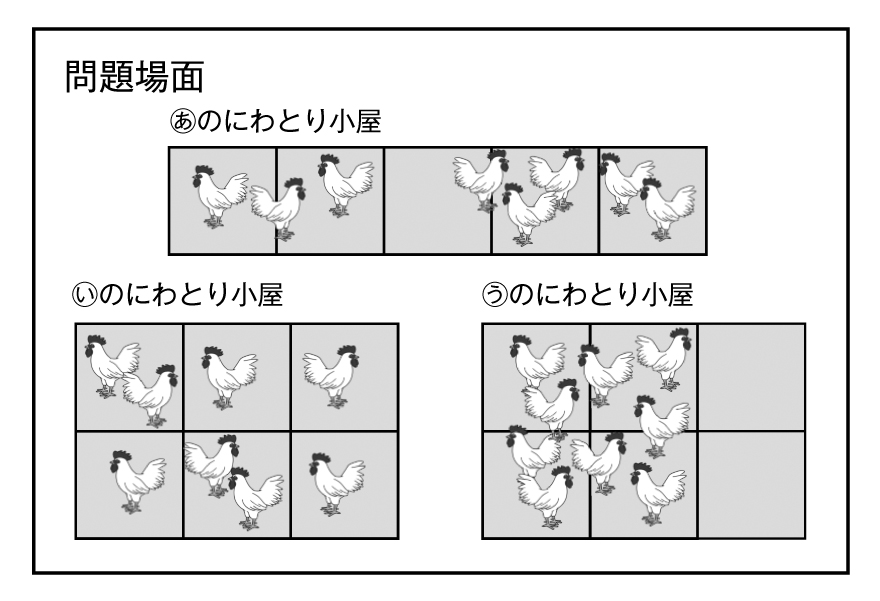
どのにわとり小屋が、一番混んでいますか。
にわとりの数が多いのは(う)の小屋だよ。
でも、(あ)の小屋は狭いよ。
小屋の面積を教えてほしい。
正方形の板1枚が1㎡です。
(あ)は5㎡、(い)と(う)は6㎡だね。
(い)と(う)はどちらも6㎡で、(い)には8羽、(う)には9羽いるから、(う)の小屋が混んでいます。
同じ面積なら、にわとりの数が多いほうが、混んでいることになるんだね。
(あ)と(い)だと、(あ)が混んでいることになると思う
よ。
(あ)と(い)は、にわとりの数はどちらも8羽だけど、(あ)の小屋のほうが狭いものね。
(あ)と(う)では、どちらの小屋が混んでいるのでし
ょうか。
にわとりの数も小屋の面積も違うから、比べられない。
本時の学習のねらい
面積もにわとりの数もちがう、にわとり小屋のこみ具合を比べる方法を考えよう。
見通し
どちらの小屋が込んでいるのか、比べるにはどうすればよいでしょうか。
面積かにわとりの数が同じときは、比べられるけれど……。
面積が5㎡と6㎡だから、どちらも30㎡にそろえられそう。
面積をにわとりの数でわると、1羽分の面積がわかるな。
自力解決の様子

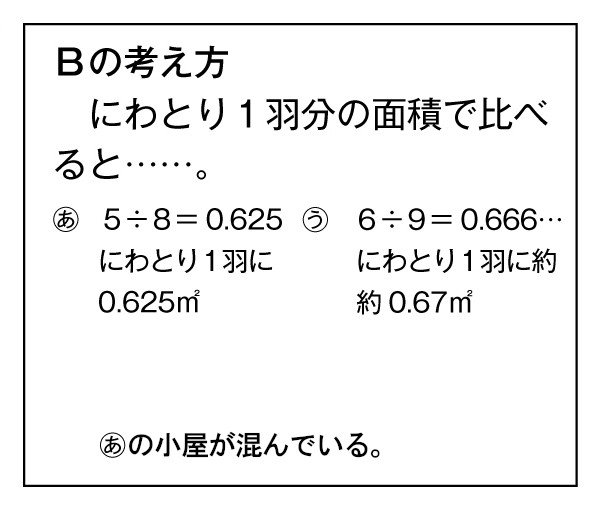

学び合いの計画
イラスト/やひろきよみ
『教育技術 小五小六』 2019年11月号より