小2算数「かけ算(2)」指導アイデア《九九表からきまりを見付ける活動を通して、乗法の計算に関して成り立つ性質を理解する》

執筆/新潟⼤学附属⻑岡⼩学校教諭・稲葉謙太郎
監修/東京都国立教育政策研究所教育課程調査官・加固希支男、新潟県新潟市立上所小学校教諭・志田倫明
目次
年間指導計画
・表とグラフ
・時刻と時間
・2けたのたし算
・2けたのひき算
・長さ
・1000までの数
・水のかさ
・大きい数のたし算とひき算
・三角形と四角形
・式と計算
・かけ算(1)
・かけ算(2)
・かけ算(3)
・1000より大きい数
・たし算とひき算の関係
・図を使って考えよう
・分けた大きさ
・箱の形
単元の展開(各時の主な学習活動内容)
第1時 6の段の九九を構成する。
第2時 6の段の九九の呼称を知り、唱える。
第3時 7の段の九九を構成する。
第4時 7の段の九九の呼称を知り、唱える。
第5時 8の段の九九を構成する。
第6時 8の段の九九の呼称を知り、唱える。
第7時 9の段の九九を構成する。
第8時 9の段の九九の呼称を知り、唱える。
第9時 1の段の九九を構成する。
第10時 問題文の仕組みを読み取って加法や減法・乗法の演算決定をし、乗法の理解を深める。9の段の九九の呼称を知り、唱える。
第11時 学習内容の定着を確認するとともに、数学的な見方・考え方についてふり返る。
第12 時(本時)九九表からきまりを見付ける活動を通して、乗法の計算に関して成り立つ性質を理解する。
第13 時 情報の性質やきまりを用いて、簡単な場合の2位数と1位数の乗法の答えの求め方を考え、説明する。
第14時 「倍」についての理解を深める。
第15 時 乗法九九を総合的に活用して、物の数の求め方をかけ算を用いて解決できるように工夫して考え、説明する。
第16時 まとめ
本時のねらい
九九表からきまりを見付ける活動を通して、乗法の計算に関して成り立つ性質について理解する。
評価規準
3マス×3マスの表が九九表のどこに当てはまるのかを、乗法の計算に関して成り立つ性質を使って、説明することができる。
本時の教材のポイント
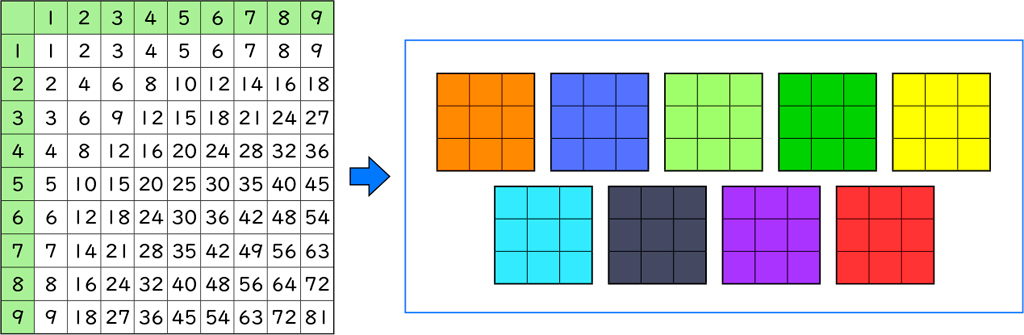
ここでは、これまでに学習した乗法九九を基に学習を進めていきます。まず、これまでの学習をふり返り、九九表は1~9の段の乗数が1の場合の積を左端に揃え、被乗数分の数だけ足して、右に書き込むことで完成させられることを確認します。
次に、九九表の数字を隠し、3マス×3マスに切ってできた9枚の小さな表をバラバラにして提示します。「もとの九九表に戻しましょう」と問いかけることで、数字が見えないため、それぞれの表がもともと九九表のどの部分に当たるのか判断できないことを確認します。
そこで、各表の左上の1マスだけ開いて、数字を1つだけ見せます。例えば、左上に「1」が表示されている表を提示すると、多くの子供が、その表が九九表の左上の部分であることに気付きます。理由を問うことで、「1」は「1×1=1」を表していることを確認します。このように、3マス×3マスに分けた表でも、左上の数字を見ることで、九九表のどの部分に当たるかを判断できることを確かめます。
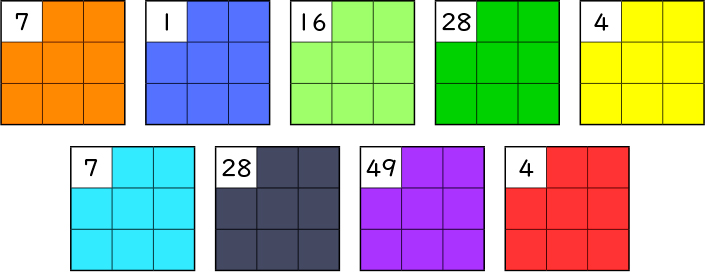
続いて、他の表の左上も全て表示します。子供は「16」や「49」といった数字に着目し、「4×4=16」「7×7=49」と判断していきます。しかし、「4」や「7」のように、九九表の中に何度か出てくる数の場合、左上の数字だけでは九九表の位置を特定できないことに気付きます。
ここで、「なぜ九九表の中に同じ数があるのだろう」と問いかけます。子供からは「7は『1×7』と『7×1』のどちらもあるから」といった意見が出され、乗数と被乗数を入れ替えても積が等しいことを共有します。
次に、1つの表を取り上げて、「あとどこのマスの数を知りたいですか」と問いかけます。例えばオレンジ色のマスでは、子供から次のような考えが出されることが予想されます。
・全てのマスが見たい。九九表と同じ数か確かめられるから。
・7と同じ横の列が見たい。何の段の答えか分かるから。
・7の右のマスが見たい。「1×7+1=8」のように増え方が分かるから。
実際に順番にマスをめくり、どの時点で位置を判断できるか確かめます。「7」の右側をめくると数の増え方を手がかりに、オレンジ色の表が九九表のどこに位置するかを判断できることが分かります。
その後、他の色の表についても位置を考えていきます。子供は「横にめくればすぐ分かる」「いくつずつ増えているかが分かれば位置が分かる」など、オレンジ色の表の位置を考えるときに共有した見方・考え方を生かしながら、発展的に考察していく姿が期待できます。
本時の展開
これは九九の答えがすべて書いてある「九九表」です。九九表を見ながら九九を唱えてみましょう。
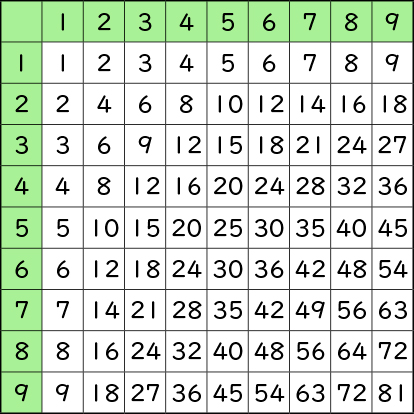
1×1が1、1×2が2……。
各段の答えが、左から右へ横に並んでいますね。今日は九九表の数を隠して、3×3マスの表に切ってしまいます。

わあ、3マスずつに分かれている。
9つ表ができたね。
バラバラにした表は、どこに入るでしょう。
えー、さすがに分からない。
隠れている数を見せてほしい。
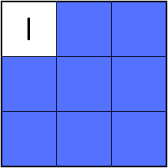
そうですね。では、青い表の1マスだけ開けてみました。これならどうでしょう。

分かった。いちばん上だ。だって、「1」は1×1=1だから。
1になる答えは1つしかない。

他の表も1マスの数が分かれば、どこの場所か分かりそう。
1マスだけめくれば、見付けることができましたね。他の表も1マスだけ開けて、九九表のどこに位置するのか調べてみましょう。

全部分かりそう。
「16」は「4×4=16」の場所だね。
「49」は「7×7=49」の場所だ。
「7」は「1×7=7」の場所かな。
あれ、「7」が2枚あるよ。オレンジと水色はどちらも「7」だ。
「28」と「4」も2枚ある。
どうして2枚もあるの? 先生間違えちゃったのかな。
「7」は「1×7」だけじゃなくて「7×1」もある。
「4」は「1×4」と「4×1」と「2×2」がある。
「2×2」はさっきの青い表にもう入っているよ。
掛ける数と掛けられる数を入れ替えても答えは同じだから、2つあるんだ。
もっとめくらないと九九表のどこなのかはっきりしない。
では、左上が「7」のオレンジ色の表で考えてみましょう。どこに当てはまるのかを調べるには何枚めくればいいでしょうか。
全部かな。
全部はいらない。
1枚でもいいよ。
それでは、どこをめくれば九九表に当てはめることができるのか考えてみましょう。

オレンジ色のひょうの場しょをはっきりさせるには、どこをめくればよいかな。
自力解決の様子
A つまずいている子
・オレンジ色の隠れている部分を全てめくって、九九表のどこに当てはまるのかを見付けようとしている。きまりを使えばよいことに目が向いていない。
B 素朴に解いている子
・横をめくれば、いくつずつ増えているのかが分かるから何の段か分かる。
・縦をめくれば、他の2列も何の段か分かりそうだ。
C ねらい通り解いている子
・「7」は「7×1=7」と「7×1=7」がある。だから、1の段か7の段かが分かればいい。
・横を1枚めくれば、いくつずつ増えるのかが分かる。
全体発表とそれぞれの考えの関連付け
それでは発表してもらいます。どこをめくって調べようと思いましたか。
全てをめくって調べようと思います。そうすると、九九表と同じ数の並びを見付けることができます。でも、全てめくるので大変です。
全てめくると、確かに九九表の並びがはっきりしますね。縦と横をめくっている人もいましたね。
私は縦だけ見れば分かると思います。上から順に1~9の段が並んでいるので、縦をめくれば、「7」の下が何の段か分かると思いました。
私は「7」の横をめくれば分かると思いました。横をめくるといくつずつ増えているのかがはっきりすると思いました。
確かに。何の段なのかが分かれば、九九表のどこになるのかが分かりそうです。
だったら、横を1枚めくれば、いくつずつ増えているのかが分かるので1枚でいいです。
それでは、オレンジ色の表をみんなの個人用PCに送付します。どこをめくれば場所がはっきりするのか自分で確かめてみましょう。
本当に1つだけめくれば分かるのかな。
「7」の隣は「8」だった。ということは1の段で「1×7=7」「1×8=8」ということだ。1ずつ増えているのは、掛けられる数が1だからだ。
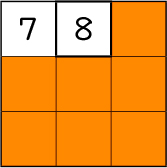
「7」の下は「14」だった。「1×7=7」の下が「2×7=14」っていうことだ。
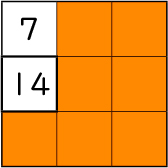
掛ける数が7だから、その分増えているということだ。
あと1枚だけめくれば、何の段かはっきりするね。
では他のカードも分かりそうですか。「4」の黄色の表と赤の表をみんなの個人用PCに送付します。どこをめくれば場所がはっきりするのか考えて、自分で確かめてみましょう。
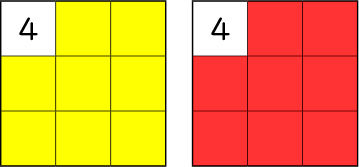
「4」の隣のマスをめくって、1ずつ増えているか4ずつ増えているか確かめてみよう。
「4」の下のマスをめくって、4ずつ増えているか1ずつ増えているか確かめてみよう。
まとめ
構成/桧貝卓哉 イラスト/横井智美 図版作成/永井俊彦

